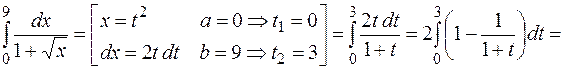
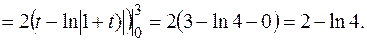
Решение. Интегрирование по частям в определенном интеграле.Пусть 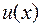и

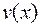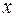Интегрирование по частям в определенном интеграле. Пусть и — дифференцируемые на отрезке функции перемен­ной . Тогда

.

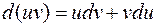Проинтегрируем обе части послед­него равенства на отрезке

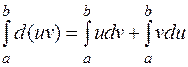
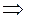
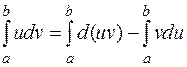
По формуле Ньютона — Лейбница

.

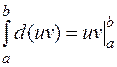Следовательно,

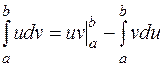
Эта формула называется формулой интегрирования по частям в определенном интеграле.

Пример. Вычислить .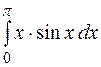

Решение. Применим формулу интегрирования по частям в определенном интеграле

.

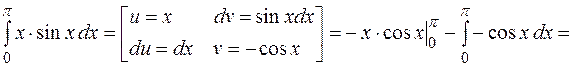
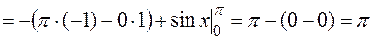Вычисление площадей плоских фигур