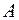Пусть требуется вычислить площадь фигуры, ограниченной линией 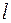 , заданной в полярной системе координат
, заданной в полярной системе координат 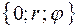 уравнением
уравнением 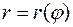 ,
, 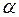 b
b 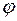 b
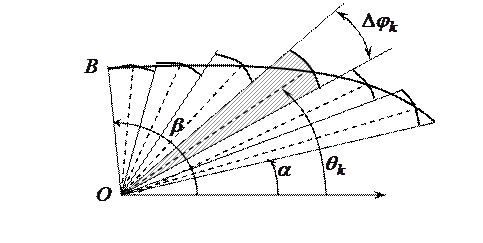
b 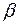 . За базовую фигуру в полярной системе координат принимается криволинейный сектор — фигура, ограниченная линией
. За базовую фигуру в полярной системе координат принимается криволинейный сектор — фигура, ограниченная линией 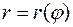 и радиусами-векторами
и радиусами-векторами 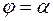 ,
, 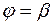 . При этом криволинейный сектор будем считать правильной фигурой, т. е. такой, что любой луч
. При этом криволинейный сектор будем считать правильной фигурой, т. е. такой, что любой луч 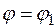 ,
, 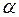 b
b 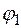 b
b 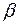 , исходящий из полюса
, исходящий из полюса 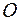 , пересекает линию
, пересекает линию 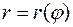 не более, чем в одной точке. Будем также предполагать, что функция
не более, чем в одной точке. Будем также предполагать, что функция 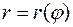 непрерывна на отрезке
непрерывна на отрезке 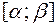 .
.
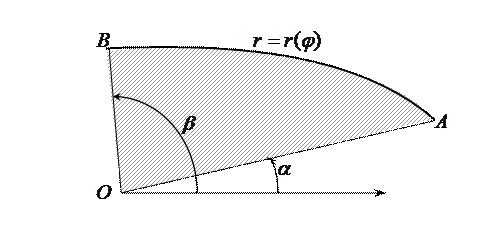
Для вычисления площади криволинейного сектора 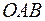 применим алгоритм составления интегральной суммы с последующим предельным переходом к определенному интегралу.
применим алгоритм составления интегральной суммы с последующим предельным переходом к определенному интегралу.
1. Разобьем отрезок 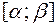 на
на 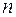 частичных отрезков точками
частичных отрезков точками 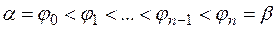 . Обозначим
. Обозначим 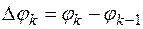 ,
, 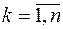 . Проведем лучи
. Проведем лучи 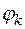 ,
, 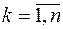 . Тогда криволинейный сектор
. Тогда криволинейный сектор 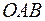 разобьется на
разобьется на 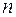 частичных криволинейных секторов.
частичных криволинейных секторов.
2. На каждом частичном отрезке 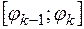 , выберем произвольным образом точку
, выберем произвольным образом точку 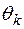 и найдем значения функции
и найдем значения функции 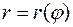 в этих точках:
в этих точках: 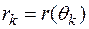
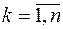 .
.
|
3. Предположим, что на каждом из частичных отрезков 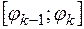 функция
функция 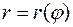 постоянна и совпадает со значением
постоянна и совпадает со значением 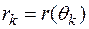 . Тогда каждый частичный криволинейный сектор можно заменить круговым сектором с радиусом
. Тогда каждый частичный криволинейный сектор можно заменить круговым сектором с радиусом 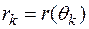 и центральным углом
и центральным углом 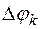 . Площадь такого кругового сектора вычисляется по формуле
. Площадь такого кругового сектора вычисляется по формуле
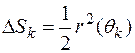
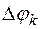 .
.
Тогда
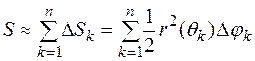 . (1)
. (1)
Приближенное равенство тем точнее, чем меньше частичные отрезки, т. е. чем больше 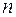 .
.
4. За точное значение площади S криволинейного сектора 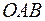 можно принять предел интегральной суммы (1) при
можно принять предел интегральной суммы (1) при 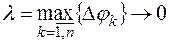 .
.
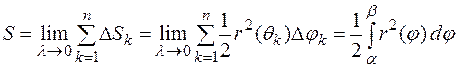 .
.
Таким образом, площадь криволинейного сектора вычисляется по формуле
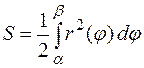 .
.
Пример. Вычислить площадь фигуры, ограниченной 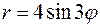 ,
, 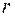 r0.
r0.
Решение. Найдем область определения данной функции.
 r0
r0
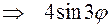 r0
r0
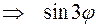 r0
r0
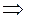
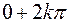 b
b 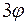 b
b 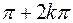
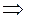
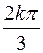 b
b 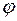 b
b 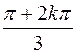 ,
,
при 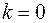
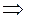
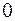 b
b 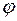 b
b 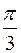 ,
,
при 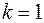
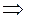
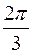 b
b 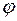 b
b 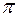 ,
,
при 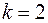
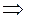
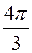 b
b 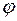 b
b 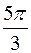 ,
,
при 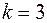
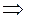
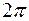 b
b 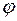 b
b 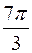 ,
,
На интервале от 0 до 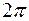 функция
функция 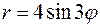 определена на трех участках. Изобразим график функции на рисунке.
определена на трех участках. Изобразим график функции на рисунке.

Так как функция периодическая, то
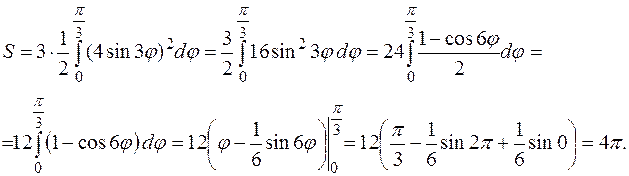
 2015-06-04
2015-06-04 623
623