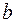В прямоугольной системе координат

Из геометрического смысла определенного интеграла следует, что если 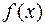r0 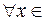,то площадь криволинейной трапеции, ограниченной кривой 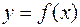,осью 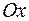и прямыми 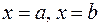, может быть вычислена по формуле

.

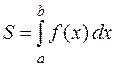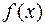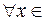
Если b0 , то

.

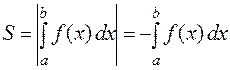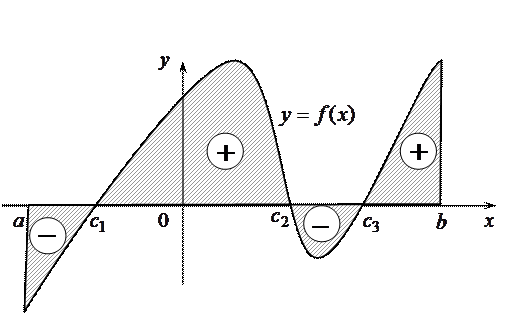
Если подынтегральная функция конечное число раз меняет знак на отрезке ,то площадь заштрихован­ной на рисунке фигуры 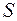равна алгебраической сумме площадей соответствующих криволинейных трапеций, лежа­щих над осью 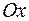(со знаком «+») и под этой осью (со знаком «—»).

Для того чтобы получить общую площадь заштрихован­ной отрезок интегрирования надо раз­бить на частичные отрезки, на которых функция сохраняет знак, то есть

.

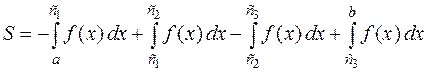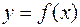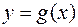
Если надо вычислить площадь фигуры, ограниченной линиями , , 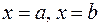то эту площадь рассматривают как разность площадей двух криволинейных трапеци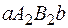й и 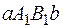. В этом случае

,

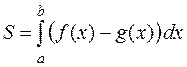если r .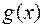

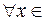
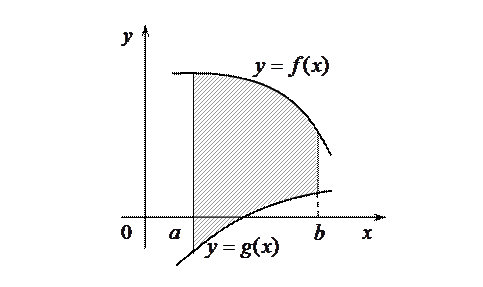
В случае, когда разность 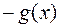не сохраняет знак на отрезке , этот отрезок разбивают на частичные отрезки, на каждом из которых функция 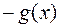сохраняет знак.

Пример. Определить площадь фигуры, ограниченной кривыми , , .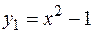

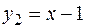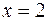Решение. Решив систему уравнений

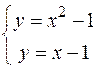
найдем точки 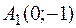, 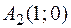пересечения параболы 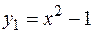и прямой .

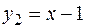Следовательно,

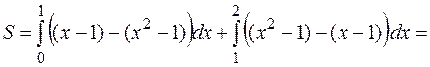
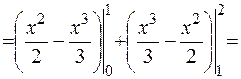
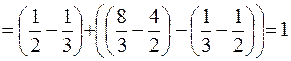(кв.ед.)