Формула Ньютона-Лейбница

Теорема. Значение определенного интеграла на отрезке от непрерывной функции равно разности значений любой ее первообразной, вычисленной пр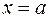и и :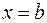

.

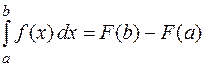Доказательство. Пусть функция , непрерывная на отрезке , следовательно, она имеет на этом отрезке первообразную, например

.

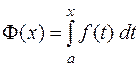Пусть 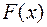— любая другая первообразная функция на том же отрезке . Так как первообразные 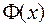и 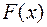отличаются друг от друга постоянным слагаемым, то имеет место равенство

, , .

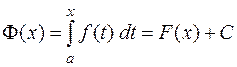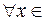
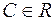Подставляя в это равенство значение 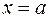, получим

.

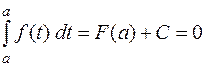
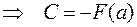Полагая 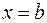и обозначая переменную интегрирования через 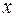, получаем основную формулу интегрального исчисления:

.

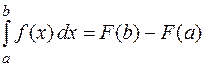которая называется формулой Ньютона — Лейбница.

⊠

Формула Ньютона — Лейбница позволяет избавиться от вычисления определен­ных интегралов как пределов интегральных сумм, и задача вычисле­ния определенного интеграла сводится к задаче вычисления не­определенного интеграла.