Приведем без доказательства три теоремы, с помощью которых можно исследовать вопрос о сходимости некоторых несобственных интегралов первого рода.
Теорема. (признак сравнения). Если на промежутке [ 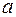 ;+¥[ определены две неотрицательные функции
;+¥[ определены две неотрицательные функции  и
и 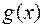 , интегрируемые на каждом конечном отрезке
, интегрируемые на каждом конечном отрезке  , причем 0b
, причем 0b  b
b 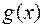 для
для 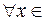 [
[ 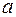 ;+¥[, то из сходимости интеграла
;+¥[, то из сходимости интеграла 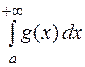 следует сходимость интеграла
следует сходимость интеграла 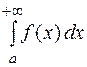 ,а из расходимости интеграла
,а из расходимости интеграла 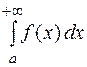 следует расходимость интеграла
следует расходимость интеграла 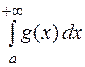 .
.
Теорема (предельный признак сравнения). Если на промежутке [ 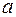 ;+¥[ определены две положительные функции
;+¥[ определены две положительные функции  и
и 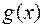 , интегрируемые на любом конечном отрезке
, интегрируемые на любом конечном отрезке  , и существует конечный предел
, и существует конечный предел
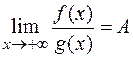 ,
,
то несобственные интегралы 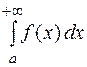 и
и 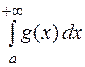 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Теорема. Если на промежутке [ 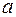 ;+¥[функция
;+¥[функция 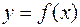 меняет знак и несобственный интеграл
меняет знак и несобственный интеграл 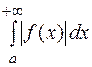 сходится, то сходится также и
сходится, то сходится также и 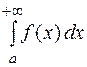 .
.
Отметим, что несобственный интеграл 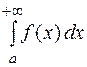 называют абсолютно сходящимся, если сходится интеграл
называют абсолютно сходящимся, если сходится интеграл 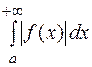 .
.
 2015-06-04
2015-06-04 341
341








