Неограниченных функций (второго рода)

Определение. Несобственным интегралом от функции , непрерывной на промежутке 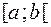и имеющей бесконечный разрыв в точке 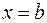, или несобственным интегралом второго рода называется предел интеграла 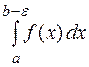при :

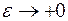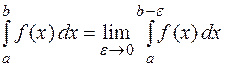. (4)

Аналогично если функция имеет бесконечный разрыв в точке 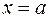, то полагают

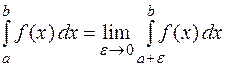. (5)

Если же функция имеет разрыв второго рода в некоторой внутренней точке отрезка 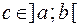, то, пользуясь свойством адди­тивности определенного интеграла, данный интеграл пред­ставляют в виде суммы двух интегралов:

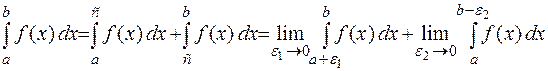.(6)

Если пределы в правых частях формул (4) — (6) суще­ствуют и конечны, то соответствующие несобственные интегралы от разрывной функции в точках 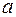, 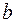и 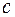называются сходящимися, в противном случае — расходящимися.

С геометрической точки зрения сходящийся несобственный ин­теграл второго рода означает, что фигура, ограниченная кривой 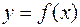r0, прямыми 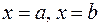, 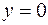и бесконечно вытянутая в направлении оси 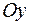имеет конечную площадь .

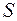Пример. Исследовать на сходимость несобственный интеграл .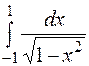

Решение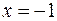. При и при 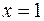подынтегральная функция имеет бесконечный раз­рыв, следовательно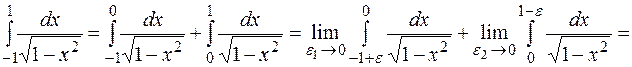

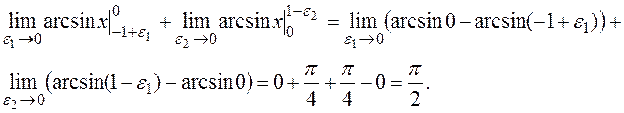
Итак, несобственный интеграл сходится и определяет площадь 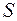бесконечной криволинейной трапеции, изображенной на рисунке.

Пример. Исследовать на сходимость несобственный интеграл .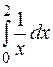

Решение. При 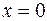подынтегральная функция имеет бесконечный раз­рыв, следовательно 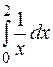является несобственным интегралом второго рода, тогда по определению

+¥.

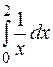
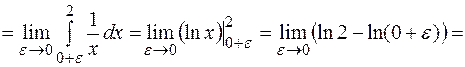т. е. несобственный интеграл расходится.

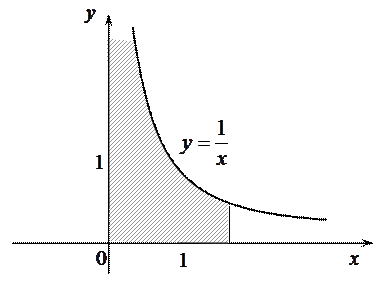
Геометрически это означает, что площадь криволинейной трапеции, изображенной на рисунке, не ограничена.