Функция распределения вероятностей F(x): ее определения и свойства

Опр.: ф-я распределения СВ называется ф-я F(x)выражающая для каждого Х вероятность того, что Хпримет значение, меньшее х: F(x) = P(Х<x)

Ф-я F(x) - интегральная ф-я распределения.

Св-ва ф-ии F(x):

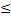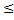1) 0 F(x) 1;

2) F(x)-неубывающая ф-я на всей числовой оси;

3) F() =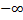

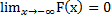
F() =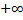

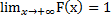
4) P(x₁ 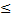x 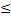x₂)=F(x₂) - F(x₁)

Распределение случайной величины 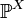однозначно определяет функцию распределения.

Верно и обратное: если функция 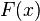удовлетворяет четырём перечисленным выше свойствам, то существует вероятностное пространство и определённая на нём случайная величина, такая что 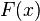является её функцией распределения.

По определению непрерывности справа, функция 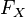имеет правый предел 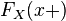в любой точке 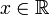, и он совпадает со значением функции 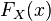в этой точке.

В силу неубывания, функция 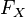также имеет и левый предел 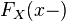в любой точке 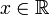, который может не совпадать со значением функции. Таким образом, функция 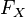либо непрерывна в точке, либо имеет в ней разрыв первого рода.