Применяется для решения задач с кусочно-непрерывным (кусочно-постоянным) управлением. Наиболее часто используются в случае, когда управление ограничено по величине 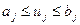 и функционал линейно зависит от управления. Также, как и задачи классического вариационного исчисления по уравнениям ограничений и целевой функции записывают функцию Гамильтона, записывают систему уравнений Эйлера (Эйлера-Лагранжа, Эйлера-Гамильтона) и управляющее воздействие ищут таким образом, чтобы функция Гамильтона в каждый момент времени в явном виде имело максимальный уровень при изменении
и функционал линейно зависит от управления. Также, как и задачи классического вариационного исчисления по уравнениям ограничений и целевой функции записывают функцию Гамильтона, записывают систему уравнений Эйлера (Эйлера-Лагранжа, Эйлера-Гамильтона) и управляющее воздействие ищут таким образом, чтобы функция Гамильтона в каждый момент времени в явном виде имело максимальный уровень при изменении 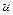 . Это возможно только тогда, когда функции
. Это возможно только тогда, когда функции 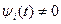 на некотором интервале
на некотором интервале 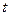 . И
. И 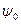 принимают
принимают 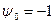 , если исходный функционал минимизировался. Сам предел максимума формируется следующим образом: чтобы возможное допустимое управление
, если исходный функционал минимизировался. Сам предел максимума формируется следующим образом: чтобы возможное допустимое управление 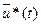 и соответствующая ему траектория
и соответствующая ему траектория 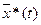 необходимо, чтобы существовало такое ненулевое решение
необходимо, чтобы существовало такое ненулевое решение 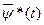 системы уравнений Эйлера
системы уравнений Эйлера 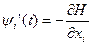 ,
, 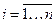 , что при любом
, что при любом 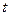 функция Гамильтона переменной
функция Гамильтона переменной 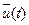 достало в точке
достало в точке 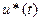 ,
, 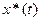 максимума, при
максимума, при 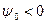 .
.
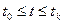 ;
;
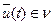 ;
;
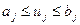 .
.
Возможным называют управление, которое обеспечивает перевод объекта из начальной в конечную точку.
Пример: 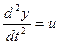 ;
;
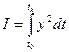 ;
;
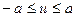 ;
;
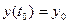 ,
, 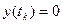 ;
;
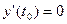 ,
, 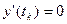 .
.
Нужно обеспечить минимум.
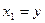 ;
;
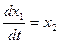 ;
;
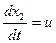 ;
;
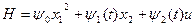 ;
;
1) 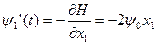
2) 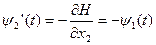 .
.
Если 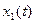 тождественно не равна нулю, то
тождественно не равна нулю, то 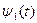 и
и 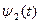 также не будут равны нулю.
также не будут равны нулю.
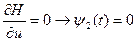 - уравнение записывать не следует, т.к. функция Гамильтона линейно зависит в явном виде от
- уравнение записывать не следует, т.к. функция Гамильтона линейно зависит в явном виде от 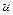 , и максимум функции Гамильтона будет достигаться при граничных значениях
, и максимум функции Гамильтона будет достигаться при граничных значениях 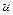 ,т.е.
,т.е.
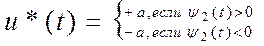 .
.
Как видно в данном случае управляющее воздействие будет кусочно-постоянным. Точку изменения знака 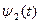 , определенную в момент переключения управления найти из системы уравнений не всегда удается, т.к. если
, определенную в момент переключения управления найти из системы уравнений не всегда удается, т.к. если 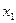 - неизвестна, следовательно,
- неизвестна, следовательно, 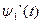 также неизвестна. Чтобы решить задачу необходимо из физических соображений выбрать начальное управление. Если
также неизвестна. Чтобы решить задачу необходимо из физических соображений выбрать начальное управление. Если 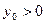 , а
, а 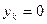 , то очевидно, что управление должно быть отрицательным:
, то очевидно, что управление должно быть отрицательным: 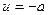 ;
;
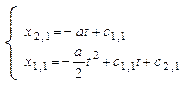
Из начальных условий находим 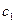 и
и  . Очевидно, чтобы в момент времени
. Очевидно, чтобы в момент времени 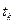 попасть в точку
попасть в точку 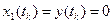 ;
;
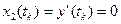 , необходимо выбрать точку
, необходимо выбрать точку 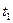 или определить ее из условия достижения нулевых значений при
или определить ее из условия достижения нулевых значений при 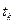 . Считаем, что с момента
. Считаем, что с момента 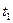 начинается второй интервал, причем
начинается второй интервал, причем 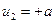 , тогда:
, тогда:
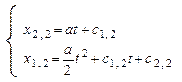
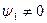 и
и 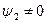 ;
;
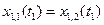 ;
;
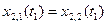 .
.
Если 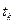 не задано, то имеем четыре неизвестных величины:
не задано, то имеем четыре неизвестных величины: 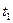 ,
, 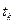 ,
, 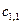 ,
, 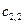 . Решая четыре уравнения, находим четыре величины и получаем точку переключения
. Решая четыре уравнения, находим четыре величины и получаем точку переключения 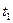 ,
, 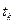 ,
, 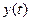 ,
, 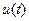 .
.
Если 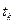 задано, тогда на четыре уравнения приходится три неизвестных, в общем случае система не имеет решения, тогда вводим еще одну точку переключения
задано, тогда на четыре уравнения приходится три неизвестных, в общем случае система не имеет решения, тогда вводим еще одну точку переключения 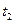 .
.
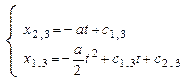 ;
;
Совместно со вторым участком получаем 6 неизвестных: 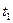 ,
, 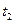 ,
, 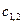 ,
, 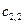 ,
, 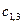 ,
, 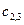 .
.
Запишем 6 уравнений:
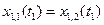 ;
;
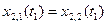 ;
;
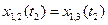 ;
;
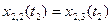 ;
;
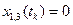 ;
;
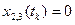 .
.
Если целевая функция или функция Гамильтона нелинейно зависят от управления: 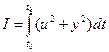 ,
,
то максимум функции Гамильтона может достигаться не на граничных значениях управления, а внутри интервала, тогда управление определяется:
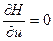 .
.
 2015-06-05
2015-06-05 634
634








