Если функционал представлен в виде:
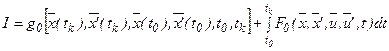 , причем верхние и нижние границы в общем случае могут быть нефиксированы, то это – задача Больца. Если
, причем верхние и нижние границы в общем случае могут быть нефиксированы, то это – задача Больца. Если 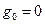 => задача Лагранжа,
=> задача Лагранжа, 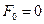 => задача Майера.
=> задача Майера.
Пример задачи Больца: Для объекта, описанного некоторой системой уравнений, найти оптимальное управление и траекторию обеспечивающих минимальный расход энергии при переводе из начального в конечное состояние за произвольное время, причем производная от координаты в конце интервала времени должны быть минимальной:
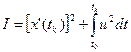 ;
;
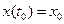 ;
;
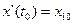 ;
;
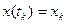 .
.
Поскольку значение искомых функций на границах интервала интегрирования, вошедшие в функцию 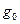 , подлежат поиску из условия обеспечения экстремума функционала, следовательно, они должны быть исключены из жестких граничных условий, т.е. их нельзя задавать численно. Недостаточные граничные условия для поиска констант интегрирования в этом случае восполняют условиями трансверсальности. Граничные условия могут быть заданы в виде гиперповерхностей, описываемых функциями
, подлежат поиску из условия обеспечения экстремума функционала, следовательно, они должны быть исключены из жестких граничных условий, т.е. их нельзя задавать численно. Недостаточные граничные условия для поиска констант интегрирования в этом случае восполняют условиями трансверсальности. Граничные условия могут быть заданы в виде гиперповерхностей, описываемых функциями 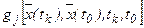
Если функционал задан или записан в результате ввода новых переменных в виде: 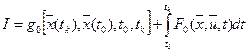 ,
,
и дифференциальные уравнения, описывающие элементы системы, так же, как и в задаче Лагранжа можно записать в форме Коши, то составляем функцию Гамильтона, а из неинтегральной части критерия и граничных условий составляем дополнительно функцию 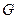 , аналогичную функции Лагранжа:
, аналогичную функции Лагранжа:
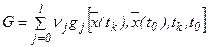 ,
,
где 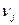 - неопределенные множители, причем
- неопределенные множители, причем 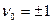 .
.
Условия трансверсальности для смешанной задачи были получены ранее из вариации функционала при изменении верхнего и нижнего пределов. Так, при вариации верхнего предела
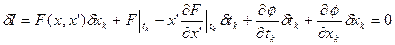 .
.
Подставляя вместо 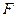 функцию Лагранжа, вместо
функцию Лагранжа, вместо 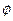 - функцию
- функцию 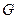 , и учитывая использование неопределенных множителей Лагранжа
, и учитывая использование неопределенных множителей Лагранжа 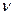 вариации
вариации 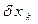 и
и 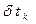 будем считать независимыми. Для независимых
будем считать независимыми. Для независимых 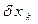 и
и 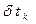 условия трансверсальности записываются:
условия трансверсальности записываются:
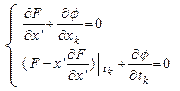 ,
,
или
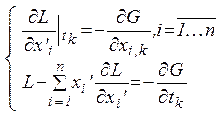
При использовании функции Гамильтона с учетом зависимостей 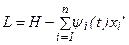 ,
, 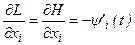 ,
, 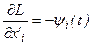 получаем:
получаем:
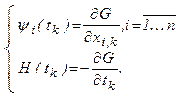
Аналогично для вариации нижней границы
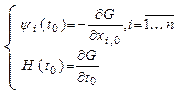 .
.
 2015-06-05
2015-06-05 2322
2322








