Теоретические основы. При наличии гетероскедастичности в остатках иногда удается получить удовлетворительные результаты т.е

При наличии гетероскедастичности в остатках иногда удается получить удовлетворительные результаты т.е. уменьшить уровень непостоянства дисперсии путем надлежащей спецификации модели. Если известна функциональная зависимость D(u_t)от одного из регрессоров может быть использован взвешенный метод наименьших квадратов [1,5,7].

Предположим, что имеет место следующая форма зависимости дисперсии от номера наблюдения:

D(u_t)= 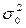(u_t) = 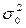·к_t;

σ(u_t) = σ₀· ,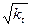

где 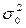– постоянная дисперсия,

к_t – некоторый коэффициент, зависящий от номера наблюдения.

Тогда если уравнение (2) разделить на 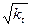, получим:

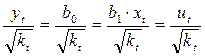. (7)

В уравнении (7) случайная компонента u_t/ 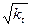= ε_t имеет постоянную дисперсию

.

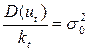Условие гомоскедастичности соблюдается. Для уравнения (7) можно использовать обычный МНК. При наличии линейной связи между к_t и x_t уравнение (7) примет вид (8). К уравнению (8) может быть использован обычный МНК.

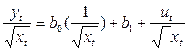. (8)

В эконометрических исследованиях довольно часто может быть выдвинута гипотеза, что значения случайной компоненты (u_t) пропорциональны значению одного из регрессоров, например, х_i в уравнении множественной регрессии

у_t = b_0,t + b₁x_1,t + … + b_ix_i,t + … u_t. (9)

Дисперсия равна

D(u_t) = · ,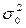

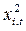Тогда

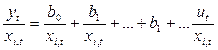. (10)

Для уравнения (10) также можно использовать обычный МНК. Характер зависимости дисперсии случайной компоненты от объясняющей переменной x можно получить с использованием теста Глейзера.

Тест Глейзера позволяет несколько более тщательно рассмотреть характер гетероскедастичности. Мы снимаем предположение о том, что σ_i, пропорционально x_i

и хотим проверить, может ли быть более подходящей какая-либо другая функциональная форма, например:

σ_i = α + β^γ_i

Чтобы использовать данный метод, следует оценить регрессионную зависимость у от х с помощью обычного МНК, а затем вычислить абсолютные величины остатков |e_i| по функции для данного значения γ. Можно построить несколько таких функций, изменяя значение γ. В каждом случае нулевая гипотеза об отсутствии гетероскедастичности будет отклонена, если оценка β значимо отличается от нуля. Если при оценивании более чем одной функции получается значимая оценка β, то ориентиром при определении характера гетероскедастичности может служить наилучшая из них.

Предположим, существует функциональная зависимость между величиной объясняющей переменной x_i и величиной модуля остатков |e_i|. Попробуем найти эту зависимость.

Предположим, что имеет место степенная зависимость |e_i| от x_i, тогда:

|e_i| = a₀ ·x_i^a1;

Найдем коэффициенты a₀ и a₁ путем логарифмирования правой и левой части, получим:

ln(e) = ln(a₀)+ a₁· ln(x);

Введем новые переменные:

Y=ln(|e_i|);

X=ln(x);

A₀=ln(a₀);

Тогда получим следующее уравнение:

Y=A₀+ a₁·X;

Используя MS Excel, построим уравнение парной регрессии и найдем значения коэффициентов A₀ и a₁. Вычислим значение a₀ по формуле:

a₀=exp(A₀).

Поделим текущие значения переменной y_i на теоретические значения |e_i| (для всех значений i) и построим уравнение парной регрессии для новой зависимой переменной (y_i/|e_i|) и прежней объясняющей переменной (x _i/|e_i|).

(y_i/|e_i|) =(b₀+b₁·x_i+u_i)/|e_i| (11)

Гетероскедастичность будет нивелирована.

Пример: построить уравнение регрессии для зависимости расходов на образование от ВВП (лабораторная работа № 5), преобразовав исходные данные согласно (11).

В случае степенной зависимости |e_i|=b₀·x^b1 получаем:

|e_i|=0,504·ВВП^0,359

А исходное уравнение в соответствии с (11) преобразуется в:

(y_i/|e_i|) =0,961+0,008·x

Данное уравнение соответствует эмпирическим данным на уровне 95,5% (R²=0,955).

Проведя проверку на наличие гетероскедастичности тестом ранговой корреляции Спирмена, получим:

r(x,e) · 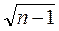= 1,68<1,96

Следовательно, при уровне значимости 0,05 для двустороннего критерия гипотеза об отсутствии гетероскедастичности будет принята.

Если допустить наличие показательной зависимости между величиной объясняющей переменной x_i и величиной модуля остатков |e_i| и провести аналогичные рассуждения получим R²=42,5%, что меньше значения коэффициента детерминации в случае степенной зависимости.

Следует признать, что новые переменные в уравнениях (7) и (10) будут иметь иное экономическое содержание.

Задание по работе:

1. Построить уравнение регрессии для зависимости расходов на образование от ВВП (лабораторная работа № 5), преобразовав исходные данные относительно регрессора х аналогично преобразованиям (7) и (11). Для этого необходимо найти параметры уравнения f(u_t²) =b₀·x^b1 , что аналогично D(u_t) = 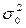·к_t. Тогда разделив обе части уравнения (2) на к_t = x^b1 можно предположить, что остатки будут гомоскедастичны.

2. Построить уравнение парной регрессии на основе обобщенного МНК для индивидуального задания к лабораторной работе № 6 в предположении, что имеет место автокорреляция 1-го порядка.

Отчет должен содержать: р езультаты моделирования по заданиям.