1. Переместительное свойство: 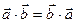
2. Распределительное свойство: 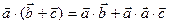
3. Сочетательное свойство относительно числового множителя:
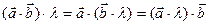
4. Скалярное произведение обращается нуль в том и только том случае, когда векторы перпендикулярны: 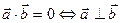
5. Так как модуль вектора, число неотрицательное, то знак скалярного произведения определяется знаком cos 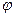 :
:
а) если 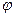 - острый угол, то
- острый угол, то 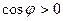 и
и 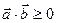
б) если 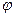 - тупой угол, то
- тупой угол, то 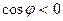 и
и 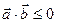
Умножение векторов в координатах. 
Даны векторы: 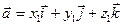
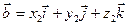
Найдём: 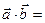 (
(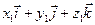 )(
)(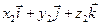 )=
)= 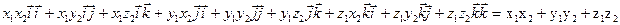
Приложения скалярного произведения
1. Длина вектора. 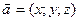 Найти
Найти 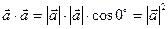
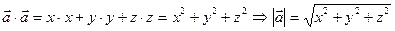
2. Расстояние между точками. 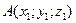 ,
, 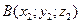

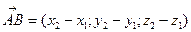
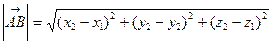
3. Угол между векторами. 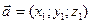
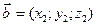
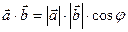
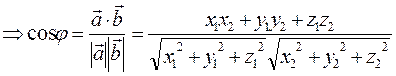
4. Проекция одного вектора на другой. 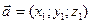
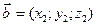
Найти 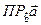
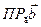
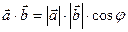 =
= 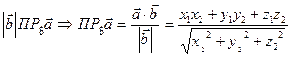
5. Условие перпендикулярности векторов.
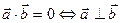
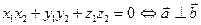
 2015-06-05
2015-06-05 612
612








