1. Смешанное произведение равно нулю если:
- хоть один из перемножаемых векторов равен нулю.
- два из перемножаемых векторов коллинеарны.
- три ненулевых вектора параллельны одной и той же плоскости (компланарность)
2. Смешанное произведение не изменится, если в нем поменять местами знаки векторного 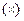 и скалярного
и скалярного 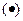 умножения.
умножения.
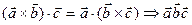
3. Смешанное произведение не изменится, если переставлять перемножаемые векторы в круговом порядке.
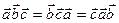
4. При перестановке любых двух векторов смешанное произведение меняет только знак:
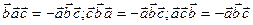
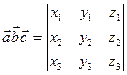
Необходимым и достаточным условием компланарности трех векторов служит условие 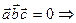 уравнение плоскости
уравнение плоскости


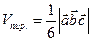
 2015-06-05
2015-06-05 365
365







