Набор из n+1 вероятностей , где kϵ
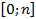 называется биномиальным распределением вероятностей, так как эти Р служат слагаемыми в разложении бинома Ньютона: (p+q)^n=1. Сумма равная 1 согласуется с постулатом 2 в аксиоматическом определении вероятности, так как это сумма всех вероятностей всех исходов данного опыта.
называется биномиальным распределением вероятностей, так как эти Р служат слагаемыми в разложении бинома Ньютона: (p+q)^n=1. Сумма равная 1 согласуется с постулатом 2 в аксиоматическом определении вероятности, так как это сумма всех вероятностей всех исходов данного опыта.
Ясно, что 1 из (n+1) вероятностей или 2 имеет максимальное значение, которое находится следующим образом.
Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов 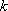 (к – наивероятнейшее число появлений события А в серии n испытаний по схеме Бернулли):
(к – наивероятнейшее число появлений события А в серии n испытаний по схеме Бернулли):
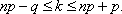
Так как 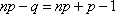 , то эти границы отличаются на 1. Поэтому
, то эти границы отличаются на 1. Поэтому 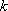 , являющееся целым числом, может принимать либо одно значение, когда
, являющееся целым числом, может принимать либо одно значение, когда 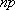 представляет собой среднее число появлений события А.
представляет собой среднее число появлений события А.
Пример. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.
Решение. Здесь 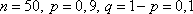 . Поэтому имеем неравенства:
. Поэтому имеем неравенства:
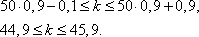
Следовательно, 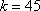 .
.
 2015-06-05
2015-06-05 1802
1802
