2015-06-05
3929
Частным случаем функциональных рядов являются степенные ряды.
Определение.
Степенным рядомназывается функциональный ряд
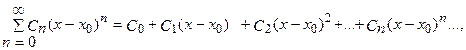(21)
члены которого являются произведениями постоянных C0 , C1 ,..., Cn,... на степенные функции от разности x-x0 с целыми неотрицательными показателями степеней, точка x0 называется центром степенного ряда.
Пример 27.
Ряд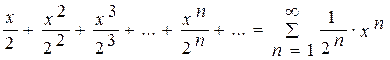 
– степенной ряд с центром в точке x0=0.
Ряд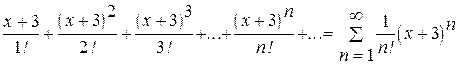 
– степенной ряд с центром в точке x0 =-3.
Ряд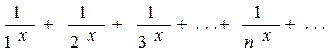 
– функциональный ряд.
Исследование степенного ряда на сходимость, а именно нахождение области сходимости степенного ряда, является одним из главных вопросов. Ответ на этот вопрос можно получить, используя теорему Абеля.
ТЕОРЕМА 10. (Теорема Абеля )
1. Если степенной ряд сходится при x=x1 (x1¹x0), то он сходится, и притом абсолютно, для всех x, удовлетворяющих неравенству
| x - x0 |<| x1-x0 |.
2. Если степенной ряд расходится при x=x2, то он расходится для всех x, удовлетворяющих неравенству
| x-x0 |>| x2-x0 |.
Опираясь на теорему Абеля можно доказать, что существует такое положительное число R, что для всех x, удовлетворяющих неравенству | x-x0 |< R, ряд сходится абсолютно и расходится при всех x, для которых | x-x0 |> R.
|
|
|
Число R называется радиусом сходимости ряда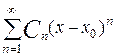 
, а интервал (x0-R, x0-R) – интервалом сходимости.
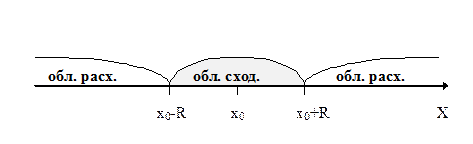
В частном случае интервал сходимости степенного ряда может совпадать со всей числовой осью (в этом случае R =¥) или может превращаться в точку (в этом случае R =0). Заметим, что интервал сходимости всегда симметричен относительно центра степенного ряда.
Пример 28. Найти интервал сходимости степенного ряда
.
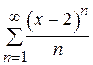Решение. Первый способ. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда: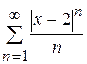 
. Применим признак Даламбера:
.
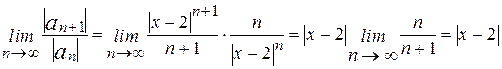Если | x -2|<1, то ряд сходится. Итак, -1< x -2<1, 1< x <3 – интервал сходимости данного ряда. Поведение данного ряда на концах интервала сходимости, т.е. в точках x =1 и x =3, исследуется отдельно.
При x =1 из данного ряда получаем ряд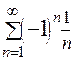 
, который условно сходится.
При x =3 получаем гармонический ряд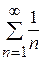 
, который расходится.
Итак, данный ряд сходится абсолютно при 1< x <3 и условно при. x= 1.
Второй способ решения. Если для степенного ряда (2) существует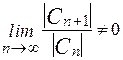 
, то радиус сходимости степенного ряда можно вычислить по формуле
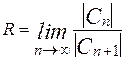. (22)
или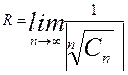 
В нашем случае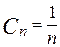 
и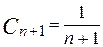 
, поэтому 
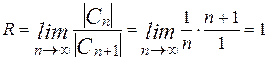. Так как x 0=2 – центр степенного ряда, то (x0-R, x0+R)=(1;3) – интервал сходимости данного ряда.
Сходимость ряда на концах интервала сходимости исследована выше.
Итак, данный ряд сходится абсолютно при 1< x <3 и условно при х =1.
