Если функция f(x) разлагается в степенной ряд по степеням (x-x0) в окрестности точки x0, то этот ряд является рядом Тейлора.
Условия разложимости функции в степенной ряд:
1. f(x) должна иметь в интервале сходимости производные всех порядков.
2. n -ая частичная сумма ряда Тейлора должна стремиться к f(х) при n ®¥, т.е. 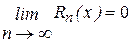 .
.
Условие 2 выполняется, если все производные f(n)(x) ограничены, т.е. если существует такое число М, что во всех точках интервала сходимости
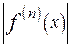 < M (nÎN).
< M (nÎN).
Сравнительная простота разложения некоторых функций в степенные ряды, привела к широкому их использованию в приближенных вычислениях. Наиболее часто используются следующие разложения элементарных функций в ряд Маклорена:
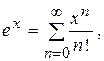
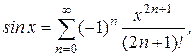
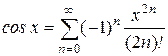 (по определению 0!=1).
(по определению 0!=1).
ln (1+ x) = 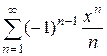 ,
,
(1+ x)a=1 + 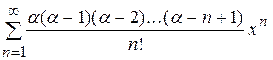 .
.
Так как область сходимости первых трех рядов xÎ(-¥,+¥), то эти равенства справедливы для любого значения x. Два последних ряда сходятся при xÎ(-1;1)
 За приближенное значение функции берется n-ая частичная сумма ряда Маклорена. При этом остаточный член ряда представляет собой абсолютную ошибку вычислений. Оценка остатка позволяет определить требуемое число слагаемых в частичной сумме. и для знакочередующегося ряда проводится на основании признака Лейбница (абсолютная величина остатка ряда не превосходит абсолютной величины первого из отбрасываемых членов ряда).
За приближенное значение функции берется n-ая частичная сумма ряда Маклорена. При этом остаточный член ряда представляет собой абсолютную ошибку вычислений. Оценка остатка позволяет определить требуемое число слагаемых в частичной сумме. и для знакочередующегося ряда проводится на основании признака Лейбница (абсолютная величина остатка ряда не превосходит абсолютной величины первого из отбрасываемых членов ряда).
Оценка остатка для знакоположительных рядов обычно производится подбором легко суммируемого ряда, члены которого больше оцениваемого остатка (чаще всего это геометрическая прогрессия).
Пример 29. Вычислить е, воспользовавшись рядом
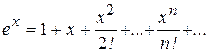
и взяв сумму первых пяти членов при х=1. Оценить величину погрешности d.
Решение. x =1. 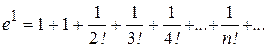
Оценим остаток данного ряда с положительными членами двумя способами.
I способ. Воспользуемся остаточным членом формулы Тейлора в форме Лагранжа
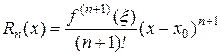 .
.
В нашем примере x0 =0, x =1, n =4, 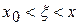 .
. 
 Поэтому
Поэтому
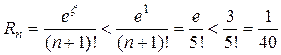 ,
, 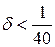 .
.
II способ.
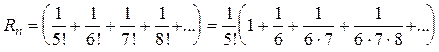 <
<
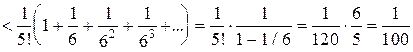 .
.
Остаток ряда d< 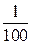 т.е. после запятой оставляем две верные цифры
т.е. после запятой оставляем две верные цифры
e»1+1+0,5+0,166+0,042»2,71.
Следует отметить, что в данном примере второй способ оценки ошибки оказался более точным.
Многие практически нужные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, так как первообразная не может быть выражена через конечное число элементарных функций.
Однако, если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат области сходимости, то можно вычислить определенный интеграл с заданной степенью точности.
Пример 30. Вычислить 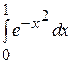 с точностью 0,0001.
с точностью 0,0001.
Решение. 1) Для разложения подынтегральной функции в ряд введем замену z=-x2 . Тогда можно использовать приведенное выше разложение в ряд Маклорена для функции вида y=ez
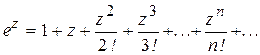 .
.
Возвращаясь к исходной переменной x, получим
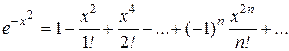 , x Î(-¥,+¥).
, x Î(-¥,+¥).
2) Проинтегрируем его почленно
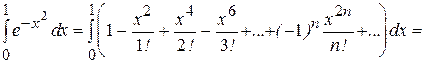
= 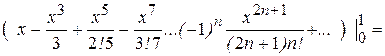
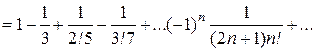
3) Получили знакочередующийся ряд. Для обеспечения требуемой точности достаточно взять сумму первых 7 членов, так как при n=6
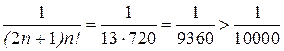 ,
,
при n =7
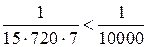 .
.
4) Вычислим приближенно интеграл с одной запасной цифрой.
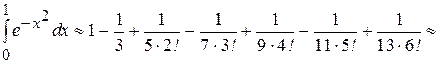
»1-0,33333+0,1-0,02381+0,00463-0,00076+0,00011=1,10474-0,35790= =0,74684.
Округляя, получим 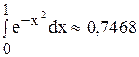 .
.
 2015-06-05
2015-06-05 720
720








