Напомним некоторые сведения из предыдущих разделов математики.
Функция называется кусочно-монотонной на отрезке 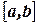 , если этот отрезок можно разбить на конечное число интервалов таким образом, чтобы в каждом из них функция была монотонной, т.е. либо не возрастающей, либо не убывающей.
, если этот отрезок можно разбить на конечное число интервалов таким образом, чтобы в каждом из них функция была монотонной, т.е. либо не возрастающей, либо не убывающей.
Функция 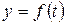 называется периодической с периодом
называется периодической с периодом 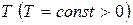 , если для любого значения аргумента из области определения функции имеет место равенство
, если для любого значения аргумента из области определения функции имеет место равенство
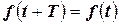 .
.
Для таких функций результат интегрирования в пределах, отличающихся на 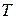 , не зависит от выбора нижнего предела интегрирования, т.е. для любого
, не зависит от выбора нижнего предела интегрирования, т.е. для любого 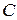
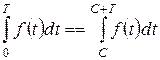 (23)
(23)
Функция 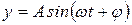 , описывающая гармоническое колебание, имеет период
, описывающая гармоническое колебание, имеет период 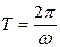 .
.
Функции 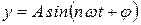 будем называть гармониками. Их можно представить также в виде
будем называть гармониками. Их можно представить также в виде
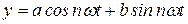 ,
,
где 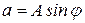 ;
; 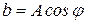 .
.
Сумма гармоник 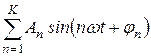 , являясь периодической, уже не будет гармоникой. Можно поставить обратную задачу. Можно ли периодическую функцию
, являясь периодической, уже не будет гармоникой. Можно поставить обратную задачу. Можно ли периодическую функцию 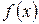 представить в виде такой суммы?. Оказалось, что при определенных условиях, сформулированных в теореме Дирихле (см. ниже), периодическую функцию с периодом
представить в виде такой суммы?. Оказалось, что при определенных условиях, сформулированных в теореме Дирихле (см. ниже), периодическую функцию с периодом 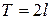 можно представить в виде суммы бесконечного числа гармоник, называемой тригонометрическим рядом.
можно представить в виде суммы бесконечного числа гармоник, называемой тригонометрическим рядом.
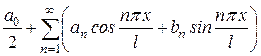 . (24)
. (24)
Если коэффициенты ряда (24) определяются по формулам
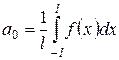 ,
,
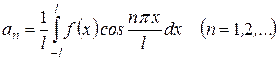 , (25)
, (25)
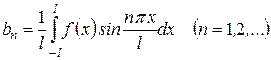 ,
,
то их называют коэффициентами Фурье, а сам ряд - рядом Фурье.
Говорят, что функция удовлетворяет условиям Дирихле, если она непрерывна на отрезке 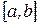 за исключением, быть может, конечного числа точек разрыва первого рода, а также кусочно-монотонна на этом отрезке.
за исключением, быть может, конечного числа точек разрыва первого рода, а также кусочно-монотонна на этом отрезке.
ТЕОРЕМА 12. (Теорема Дирихле)
Если периодическая функция 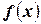 с периодом
с периодом 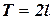 удовлетворяет на отрезке
удовлетворяет на отрезке 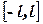 условиям Дирихле, то ряд Фурье этой функции сходится во всем отрезке
условиям Дирихле, то ряд Фурье этой функции сходится во всем отрезке 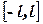 и сумма этого ряда
и сумма этого ряда 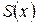 равна:
равна:
1) 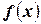 во всех точках непрерывности функции
во всех точках непрерывности функции 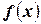 ;
;
2) полусумме пределов функции слева и справа, т.е., если 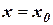 является точкой разрыва первого рода, то.
является точкой разрыва первого рода, то.
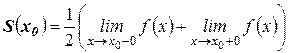 .
.
Из теорем (11) и (12) следует, что класс функций представляемых в виде ряда Фурье шире класса функций, разлагаемых в ряд Тейлора, так как для последнего необходимо существование производных функций любого порядка.
В ряде практических задач электросвязи рассматриваются периодические функции с 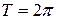 . Тогда
. Тогда 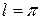 и формулы 24-25 упрощаются
и формулы 24-25 упрощаются
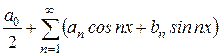 (26)
(26)
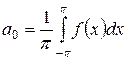 ,
,
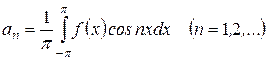 , (27)
, (27)
 .
.
Замечания:
1. Учитывая формулу (23), при нахождении коэффициентов Фурье целесообразно в качестве пределов интегрирования использовать границы области задания функции. Например, если 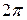 - периодическая функция задана на отрезке
- периодическая функция задана на отрезке 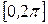 , в формулах (27) следует интегрировать от нуля до
, в формулах (27) следует интегрировать от нуля до 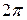 .
.
2. Если функция 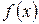 - четная, то коэффициенты
- четная, то коэффициенты 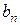 =0, а остальные коэффициенты можно найти по формулам
=0, а остальные коэффициенты можно найти по формулам
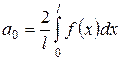 ,
, 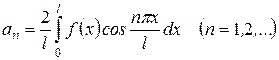 . (28)
. (28)
Если же функция - нечетная, то 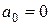 и
и 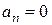 , а
, а
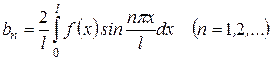 . (29)
. (29)
Ряд Фурье можно представить в амплитудно - фазовой форме. Пусть
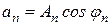 ,
, 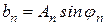 ,
,
Тогда 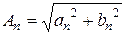 ,
, 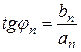 ,
, 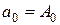 .
.
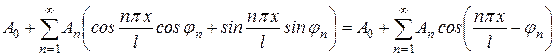 , (30)
, (30)
где 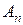 - амплитуда, а
- амплитуда, а 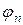 - начальная фаза
- начальная фаза 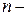 гармоники.
гармоники.
Пример 31. Разложить в ряд Фурье функцию f(x), заданную на промежутке длиной, равной периоду
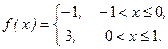

Изобразить диаграмму спектра амплитуд.
Решение. 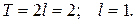
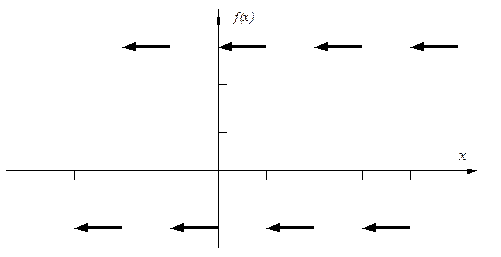
Рис. 1. График функции
По формулам (25) находим коэффициенты ряда.
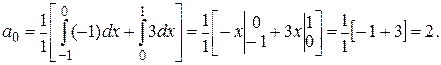
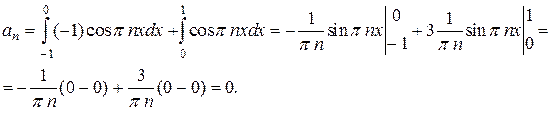
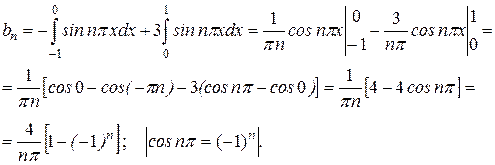
Если n - четное 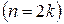 ,
, 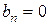 . При нечетном n
. При нечетном n 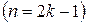
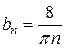 ,
,  .
.
Ряд Фурье имеет вид
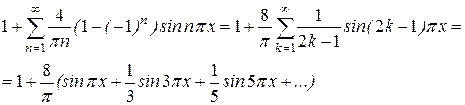
Рис. 2. иллюстрирует представления функции 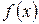 , описывающей периодический сигнал прямоугольной формы, через сумму нескольких первых членов ряда. Видно, что с ростом
, описывающей периодический сигнал прямоугольной формы, через сумму нескольких первых членов ряда. Видно, что с ростом 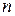 частичные суммы все точнее представляют
частичные суммы все точнее представляют 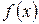 .
.
а)
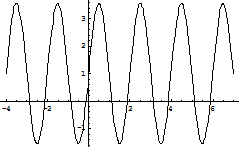
б)
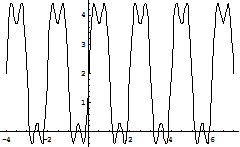
в)
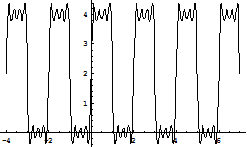
Рис. 2. Графики суммы двух(а), трех (б) и пяти(в) членов ряда
График суммы ряда 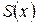 в точках непрерывности функции совпадает с графиком
в точках непрерывности функции совпадает с графиком 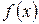 (рис. 1), а в точках разрыва
(рис. 1), а в точках разрыва 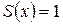 (см. теорему Дирихле). Так как
(см. теорему Дирихле). Так как 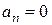 , то
, то 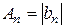 .
.
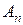
 |

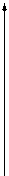
1 2 3 4 5 6 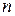
Рис.3. Спектр амплитуд
Пример 32. Разложить функцию f(x) в ряд Фурье по косинусам, продолжив в симметричный интервал. Нарисовать график суммы ряда S(x). Найти значения суммы 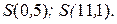
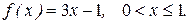

Решение. Продолжив функцию на интервале (-1,0) четным образом, и далее с периодом 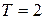 , получим сумму ряда
, получим сумму ряда 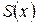 .
.
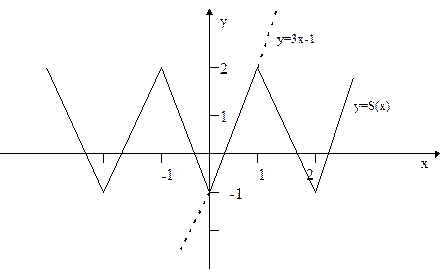
Рис. 4. Графики функций 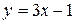 и
и 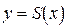
Определим коэффициенты Фурье 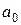 и
и 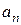 .
. 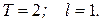
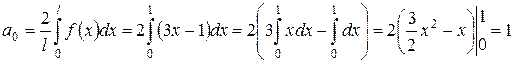 .
.
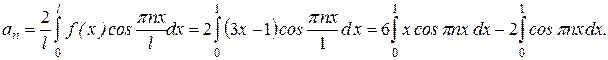 Вычислим эти интегралы отдельно, используя для первого интеграла формулу интегрирования по частям
Вычислим эти интегралы отдельно, используя для первого интеграла формулу интегрирования по частям 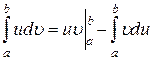 .
.
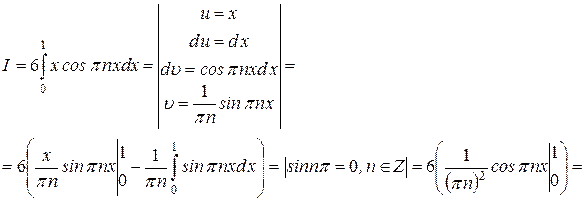
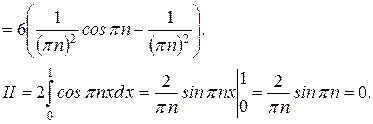
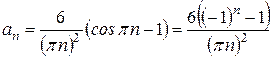 .
.
Получаем ряд Фурье:
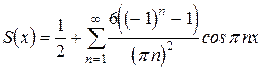
Найдем значение суммы в точках 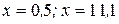 . На отрезке
. На отрезке 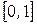
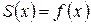 .
.
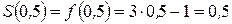 .
.
Для вычисления 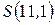 используем свойства четности и периодичности
используем свойства четности и периодичности 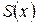 .
.
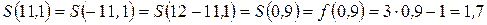 .
.
 2015-06-05
2015-06-05 1035
1035
