2015-06-26
541
Критерий конформности отображения: д ля того, чтобы отображение области D, задаваемое функцией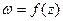 
, было конформным, необходимо и достаточно, чтобы 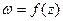была:
1) аналитической в области D,
2) 
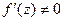всюду в D,
3) однолистной в области D функцией.
Проверим все три условия.
1) 
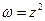– аналитическая функция всюду на плоскости Гаусса (проверяли ранее).
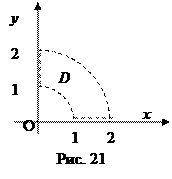2) Изобразим область D на плоскости Гаусса. 
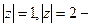уравнения окружностей с центром в точке О радиусами, соответственно, 1 и 2; 
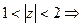– это кольцо между двумя окружностями. 
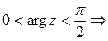область D – часть кольца, расположенная в первой четверти (рис. 21)
Найдем производную:
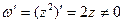для всех точек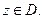 
3) Докажем, что область D – однолистная, т.е. числам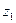 
и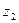 
из области D таким, что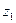 
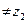, соответствуют различные значения функции 
.
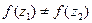Пусть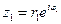 
, 
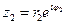(записали в показательной форме). Найдем условие, при котором 
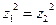, хотя .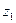 
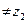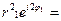
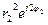. Тогда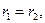 
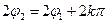, k =0,1.
Так как 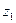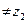, то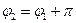 
. Следовательно, область однолистности функции 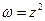не должна содержать внутри себя точек, модули которых совпадают, а аргументы отличаются на 
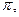т.е. областью однолистности является любая полуплоскость, например, 
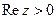или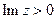 
. В нашей задаче рассматривается область, лежащая в половине полуплоскости, следовательно, D – однолистная.
Из 1) – 3) следует, что отображение, осуществляемое функцией 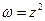, конформно в области D.
