2015-06-26
573
В теории и практике конформных отображений ставятся и решаются две задачи: прямая и обратная. Прямая задача заключается в нахождении образа данной линии или области при заданном отображении Обратная задача заключается в нахождении функции, осуществляющей отображение данной линии или области на другую линию или область.
Для решения данных задач необходимо знать некоторые свойства основных элементарных функций.
1. Линейная функция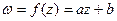 
.
a, b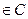 
, 
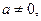т.е.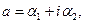 
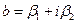. Так как 
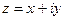, то имеем, что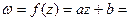 
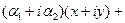
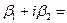
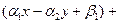
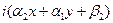. Следовательно, 
, 
.
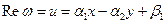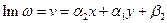1) 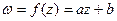– аналитическая функция, т.е. u и v – гармоническая пара, т.к. выполняются условия КРЭДа: 
, 
.
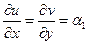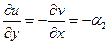2) 
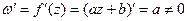для всех z .
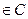Из 1) и 2) следует, что отображение, реализуемое линейной функцией, конформно на всей плоскости Гаусса.
Пусть плоскост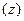и 
и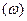 
и оси координат совпадают. Рассмотрим частные случаи.
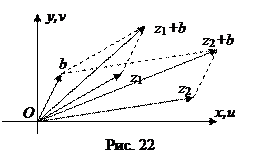1) Пусть 
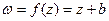(а = 1)
.
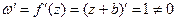Преобразование сводится к сложению переменного вектора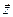 
с данным вектором 
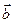, т.е. параллельному переносу плоскости 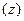на вектор 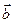(рис. 22). Поворота при этом не происходит, так как 
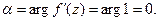Тогда
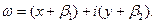
2)Пусть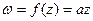 
(b = 0); 
.
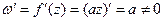Угол поворота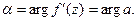 
Коэффициент растяжения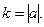 
Если а – действительное число, то поворота не происходит и вектор всякого комплексного числа растягивается в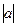 
раз, например, окружность единичного радиуса на плоскости 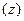превращается в окружность радиуса 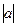на плоскости 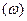, и все точки окружности перемещаются в соответствующие точки по радиусу.
Если а – комплексное число, то происходит и растяжение, и поворот одновременно.
Вывод:отображение, осуществляемое линейной функцией, представляет собой композицию растяжения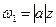 
, поворота 
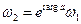и параллельного переноса 
.
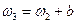Замечание 1. Обратной к линейной функции будет функция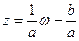 
.
Замечание 2. Отображение 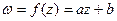конформно во всей расширенной плоскости и имеет две неподвижные точки: 
(
, 
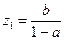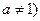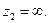
Пример 29. С помощью функции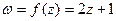 
найти отображение окружности
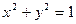на плоскость (Оuv).
