Решение. z = x + iy, = x – iy. Подставим в уравнение окружности формулы (1) и (2)

7 8 9 10 11 12 13

z = x + iy, 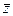= x – iy. Подставим в уравнение окружности 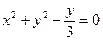формулы (1) и (2): , :

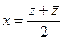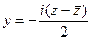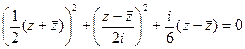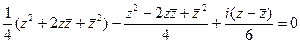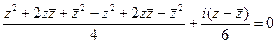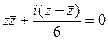Заменим 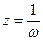, 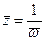. Получим:

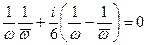
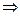
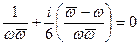
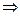
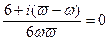
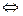
1) 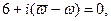2) . (*)

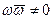Заменим 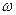на 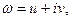и подставим в (*). Получим:

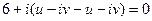
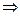
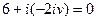
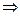
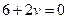
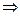
1) 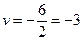– прямая.

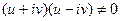
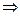
2) 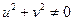( 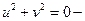точка О).

Образом окружности 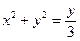при отображении 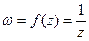будет прямая .

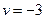Для построения окружности, приведем ее уравнение к каноническому виду:

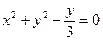
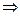
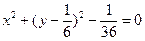
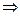центр в точке 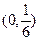, радиус – 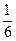(рис. 26).

3. Дробно-линейная функция 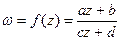, ad – bc ≠ 0, a, b, c, d .

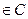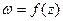может быть приведена к виду 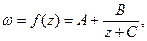где .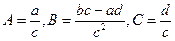

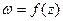– аналитическая во всей расширенной плоскости Гаусса, кроме 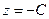. Если принять, что 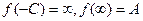, и углы между кривыми при переходе от точки 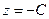к точке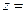 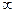и наоборот равны, то отображение будет конформно во всей расширенной плоскости Гаусса.

Геометрический смысл отображения: параллельный перенос, инверсия с полюсом в точке 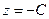, зеркальное отображение относительно прямой, проходящей через точку 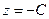параллельно действительной оси, и линейное преобразование. Другими словами, 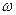представляется в виде композиции трех функций: линейной 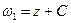, простейшей дробно-линейной 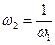и снова линейной 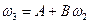. Следовательно, 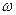также отображает окружность в окружность.

Замечание 1. Дробно-линейная функция 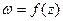вполне определяется заданием образов трех точек. Например, если 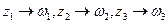, то

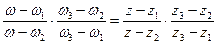. (17)

Если одна из точек 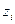или 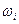является бесконечно удаленной, то в формуле все разности, содержащие эту точку, следует заменить единицами.

Замечание 2. Точки А и В, симметричные относительно прямой или окружности в плоскости (z), отображаются дробно-линейной функцией в точки А ۥ и В ۥ, симметричные относительно образа прямой или окружности в плоскости 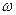. Бесконечно удаленная точка считается симметричной центру окружности.

Замечание 3. Отображение 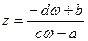, обратное к дробно-линейному, само является дробно-линейным, хотя и не совпадает с прямым отображением, т.е. не является инволюцией.