Теореми додавання та множення ймовірностей

Теорема додавання ймовірностей несумісних подій. Ймовірність появи однієї з двох несумісних подій, байдуже якої, дорівнює сумі ймовірностей цих подій:

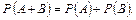
Н а с л і д о к. Ймовірність появи однієї з декількох попарно несумісних подій, байдуже якої, дорівнює сумі ймовірностей цих подій:

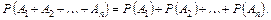
Теорема додавання ймовірностей сумісних подій. Ймовірність появи хоча б однієї з двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх сумісної появи

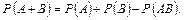
Теорема може бути узагальнена на будь-яке скінченне число сумісних подій. Наприклад, для трьох сумісних подій:

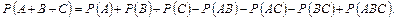
Теорема множення ймовірностей незалежних подій. Ймовірність спільної появи двох незалежних подій дорівнює добутку ймовірностей цих подій:

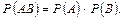
Н а с л і д о к. Ймовірність появи кількох подій, незалежних у сукупності, дорівнює добутку ймовірностей цих подій:

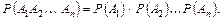
Теорема множення ймовірностей залежних подій. Ймовірність спільної появи двох залежних подій дорівнює добутку однієї з них на умовну ймовірність другої:

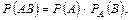
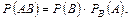
Н а с л і д о к. Ймовірність спільної появи кількох залежних подій дорівнює добутку ймовірності однієї з них на умовні ймовірності всіх інших, причому ймовірності кожної наступної події обчислюються в припущенні, що всі попередні події вже з'явилися:

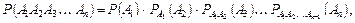
де 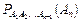– ймовірність події 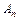, обчислена в припущенні, що події 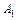, , 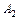, 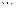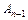настали.