2015-06-28
930
III.2. Задачи на вычисление и доказательство
Задачи с применением параллельного переноса
98. Основания трапеции имеют длины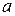 
и 
(
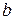), а боковые стороны при продолжении образуют прямой угол. Определить длину отрезка, соединяющего середины оснований трапеции.
99. 
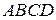- трапеция с основаниям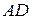и 
и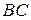 
, 
, 
. 
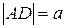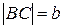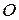- точка пересечения диагоналей трапеции. Зная, что 
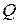- площадь данной трапеции, найти площадь треугольника 
.
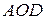100. 
, 
, 
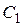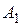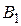- середины сторон 
, , 
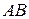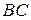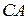треугольника 
. 
, 
, 
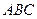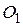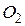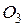- центры окружностей, описанных около треугольников 
, 
, 
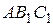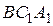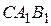соответственно. Найти длины отрезков 
, 
, 
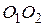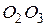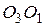, если известны длины сторон данного треугольника: 
, 
, 
.
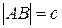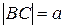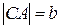101. Решить предыдущую задачу, считая, что 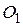, , 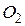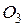- центры окружностей, вписанных в треугольники , , .
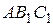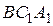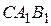102. На сторонах 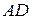и 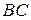параллелограмма 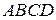построены конгруэнтные одинаково ориентированные треугольник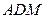и 
и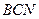 
. Найти расстояние между точкам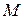и 
и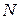 
, если известно, что 
, .
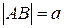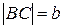103. В равнобедренной трапеции один из углов равен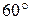 
. Доказать, что меньшее основание трапеции равно разности большего основания и боковой стороны.
104. Доказать, что в трапеции сумма оснований меньше суммы диагоналей, но больше их разности.
105. Треугольник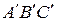 
получается из треугольника 
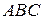некоторым параллельным переносом. Точки 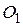и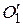 
- центры вписанных, а 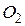и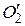 
- центры описанных окружностей для треугольников 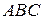и 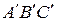соответственно. Доказать, что 
.
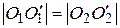106. На сторонах 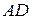и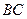 
параллелограмма 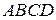построены квадраты: первый – вне параллелограмма, а второй – по ту же сторону от прямой 
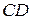, что и сам параллелограмм. Доказать, что расстояние между центрами квадратов равно длине стороны .
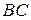107. 
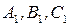– середины сторон 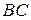, , 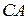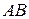треугольника ; 
, 
, 
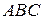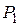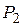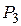- центры окружностей, вписанных в треугольники 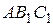, , 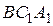, 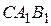а 
, 
, 
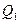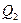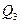- центры окружностей, описанных около тех же треугольников. Доказать, что треугольник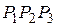и 
и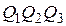 
конгруэнтны.
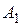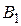108. Даны две пересекающиеся окружности равных радиусов. Секущая, параллельная линии центров этих окружностей, встречает первую окружность в точках и , а вторую – в точках 
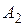и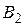 
. Доказать, что длины отрезков 
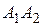и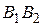 
равны расстоянию между центрами данных окружностей.
109. Две окружности равных радиусов касаются в точке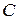 
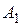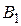внешним образом. Секущая, параллельная линии центров этих окружностей, встречает первую окружность в точках и , а вторую - в точках 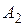и 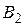. Доказать, что величина угла 
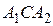не зависит от выбора секущей.
110. Две окружности равных радиусов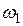 
и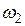 
касаются внешним образом в точке 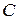. Секущая 
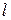, параллельная линии центров данных окружностей, пересекает окружность 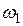в точках 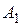и 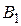, а окружность 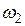– в точках 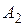и 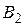. Найти величины углов 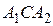и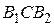 
.
111. Доказать, что два четырехугольника равны, если четыре стороны и угол, заключенный между прямыми, содержащими одну пару противоположных сторон, первого четырехугольника, равны соответствующим элементам второго.
