Задачи с применением центральной симметрии

112. Доказать, что если четырехугольник обладает центральной симметрией, то он является параллелограммом.

113. Доказать, что любая секущая, проходящая через центр симметрии параллелограмма, рассекает его на два конгруэнтных четырехугольника.

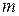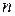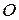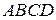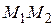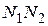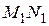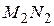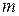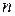114. Прямые и , проходящие через центр параллелограмма , пересекают его противоположные стороны в точках и соответственно. Доказать, что отрезки и конгруэнтны. Рассмотреть случаи: а) прямые и пересекают противоположные стороны одной и той же пары; б) прямая 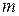пересекает противоположные стороны одной пары, а прямая 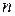- другой пары.

115. На противоположных сторонах 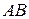и 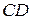параллелограмма 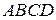от вершин 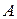и 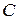отложены конгруэнтные отрезк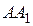и и 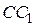. Доказать, что точк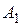и и 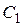лежат на одной прямой с точкой пересечения диагоналей данного параллелограмма.

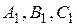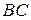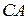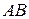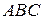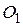116. Пусть - середины сторон , , треугольника , а и 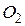- центры окружностей, вписанных в треугольник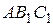и и 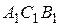. Доказать, что отрезок 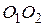делит пополам среднюю линию 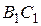данного треугольника.

117. 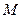- центр тяжести треугольника 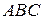; 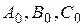- середины отрезков 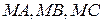соответственно. Через точки 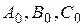проведены прямые, параллельные сторонам 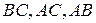данного треугольника соответственно. Доказать, что треугольник, образованный точками пересечения этих прямых, конгруэнтен треугольнику .

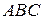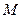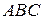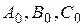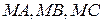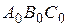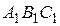118. - центр тяжести треугольника ; - середины отрезков соответственно. Доказать, что треугольники и , где 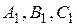- середины сторон 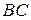, , 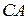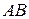данного треугольника, конгруэнтны.

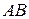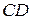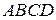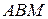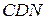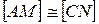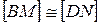119. На противоположных сторонах и параллелограмма вне его построены конгруэнтные треугольники и так, что и . Доказать, что отрезок 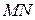проходит через точку пересечения параллелограмма и этой точкой делится пополам.

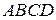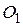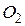120. Дан параллелограмм . Точки и - центры окружностей, вписанных в треугольник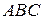и и 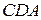. Доказать, что отрезк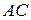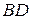и , и 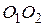пересекаются в одной точке.

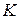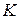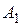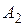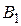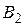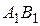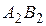121. Две окружности равных радиусов касаются в точке . Через точку проведены две секущие, одна из которых пересекает данные окружности в точках и , а другая – в точках и . Доказать, что прямые и параллельны.

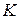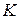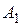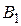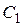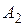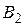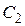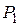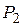122. Две окружности равных радиусов касаются в точке . Через точку проведены прямые, пересекающие первую окружность в точках , , , а вторую в точках , , соответственно. и - центры окружностей, вписанных в треугольник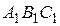и и 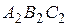. Доказать, что прямая 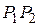проходит через точку .

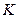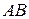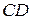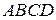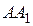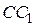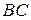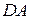123. На противоположных сторонах и параллелограмма отложены конгруэнтные отрезки и , а на сторонах и - конгруэнтные отрезки 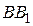и . Доказать, что четырехугольник 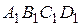- параллелограмм, центром которого совпадает с центром данного параллелограмма.

124. Из центра 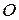параллелограмма 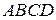опущены перпендикуляры 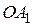, , 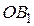, 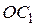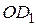на его стороны, взятые последовательно. Доказать, что четырехугольник 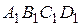является параллелограммом, центр которого совпадает с точкой .

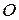125. На сторонах параллелограмма вне его построены правильные треугольники. Доказать, что центры этих треугольников образуют параллелограмм.

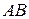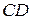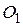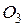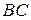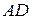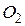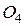126. На сторонах и параллелограмма вне его построены правильные треугольники с центрами и соответственно, а на сторонах и также вне его построены квадраты с центрами и соответственно. Доказать, что четырехугольник 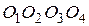– параллелограмм.