Задачи с применением гомотетии и подобия

225. Построить треугольник по двум углам и биссектрисе, проведенной из вершины меньшего из данных углов.

226. Построить треугольник 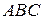по углу 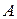и медиане 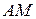, если известно, что .

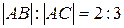227. Построить треугольник 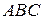по углу 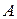и стороне 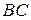, если известно, что .

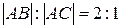228. Построить прямоугольный треугольник по гипотенузе и отношению катетов.

229. В данный треугольник вписать квадрат так, чтобы две его смежные вершины лежали на одной стороне, а остальные по одной на двух других сторонах.

230. В сектор 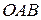данной окружности 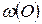вписать квадрат так, чтобы две его смежные вершины принадлежали дуге сектора, а две другие – радиусам 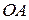и .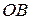

231. В данный сегмент окружности 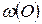вписать квадрат 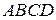так, чтобы его вершины 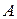и 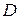лежали на хорде, а вершины 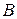и 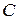– на дуге этого сегмента.

232. В данный угол вписать окружность, проходящую через данную внутри угла точку.

233. Построить треугольник по двум углам и периметру.

234. Построить треугольник по двум углам и сумме двух его высот.

235. Построить треугольник по двум углам и сумме двух его медиан.

236. Построить равнобедренный треугольник по углу при вершине и сумме основания и высоты.

237. Построить прямоугольник по стороне и отношению другой стороны и диагонали.

238. Построить ромб по стороне и отношению диагоналей.

239. Построить параллелограмм по стороне, углу между диагоналями и отношению диагоналей.

Х) Прямая, содержащая точки, и, являющиеся соответственно центром тяжести, ортоцентром и центром описанной окружности треугольника, называется прямой Эйлера по отношению к этому треугольнику.

Х) В приводимых задачах данного типа, кроме задачи 211, используются поворотные признаки равностороннего треугольника или квадрата.