Наявність спіна електрона і введення орбітального квантового числа приводять до ускладнення моделі атома. Спеціфічний рух електрона (по орбіті і власне обертання) можна описати двома моментами кількості руху: орбітальним 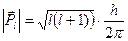 і власним механічним рухом електрона
і власним механічним рухом електрона 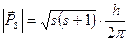 . Але кожне з цих рухів має і відповідний механічний момент, взаємодія цих магнітних моментів приводить до визначеної орієнтації механічних моментів
. Але кожне з цих рухів має і відповідний механічний момент, взаємодія цих магнітних моментів приводить до визначеної орієнтації механічних моментів 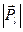 і
і 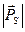 в просторі, утворенню загального механічного момента
в просторі, утворенню загального механічного момента 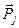 і прецесії навколо даного момента. При цьому, число можливих проекцій моментів
і прецесії навколо даного момента. При цьому, число можливих проекцій моментів 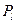 і
і 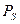 по відношенню до загального момента
по відношенню до загального момента 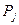 визначається через відповідні магнітні квантові числа (орбітальне ml і спінове mS):
визначається через відповідні магнітні квантові числа (орбітальне ml і спінове mS):
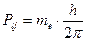 і
і 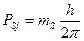 .
.
Тоді загальний момент (повний момент є вектор) буде
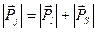 ,
,
 і для квантових чисел у вигляді векторів маємо
і для квантових чисел у вигляді векторів маємо

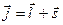 , (3.8)
, (3.8)
де j- внутрішнє квантове число, що характеризує повний механічний момент електрона в атомі (атом одноелектронний). Правило відбору для даного квантового числа
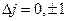 (3.9)
(3.9)
Тепер в символічних позначеннях квантових станів атомів недостатньо вказати тільки на n - головне квантове число і орбітальне квантове число - l. Внутрішнє квантове число вказують зправа внизу і значення його згідно (3.8) 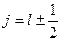 .
.
| Рівень | l (орбіт. кв. число) | Позначення |
| S | nS1/2 | |
| P | nP3/2 i nP1/2 | |
| D | nD5/2 i nD3/2 |
З врахуванням правила відбору Dj=0,±1, у Na для дифузної серії mD÷3P (m=3,4…) замість квартетів маємо триплети.
Гіпотеза Гаудсміта і Уленбека повністю пояснює дослід Штерна і Герлаха: атоми срібла знаходяться в S-стані (l=0), це означає, що орбітальний механічний момент кількості руху Pl і магнітний момент ml дорівнюють нулю, але повний магнітний момент Pj¹0, а дорівнює спіновому магнітному моменту, який може орієнтуватися паралельно або антипаралельно до зовнішнього поля, відповідно пучок розщеплюється на два, а не на три. Крім того, в досліді було показано, що відхилення пучка відповідає значенню магнітного момента рівному одному магнетону Бора mБ, тобто спіновий магнітний момент електрона дорвнює магнетону Бора
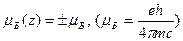 ;
;
а спіновий механічний момент кількості руху 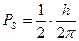 .
.
Тоді 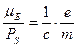 (гіромагнітне відношення). (3.10)
(гіромагнітне відношення). (3.10)
Для відношення орбітальних моментів 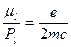 , тобто
, тобто 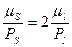 , (3.11)
, (3.11)
де 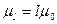 і
і 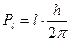 . З (3.11) випливає, що відношення власного моменту в 2 раза більше ніж для орбітального.
. З (3.11) випливає, що відношення власного моменту в 2 раза більше ніж для орбітального.
 2015-06-28
2015-06-28 1087
1087








