Задание №2. Составить уравнение прямой, проходящей через точки А и В. Будет ли принадлежать прямой точка Q?

А (4; -2), В (-3; 5), Q (0,2; 1,8)

Решение.

Составим уравнение прямой в следующем виде: ,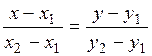

где , , , .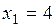

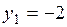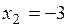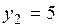Имеем: ; .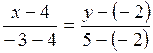

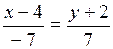Если привести уравнение к общему виду, получим: 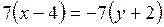или 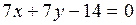. Разделив уравнение почленно на 7, получим: .

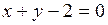Чтобы выяснить, принадлежит ли точка Q данной прямой, подставим ее координаты в уравнение: 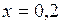, 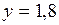: 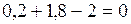. Равенство истинно, поэтому точка принадлежит прямой, проходящей через точки А и В..

Ответ. АВ: 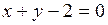, точка Q принадлежит прямой АВ.

Задание №3. Дано общее уравнение прямой. Найти:

а) угловой коэффициент прямой;

Б) отрезки, отсекаемые на осях координат, написав уравнение прямой в отрезках