Задача 1.1. Найти координаты образа 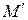 и прообраза
и прообраза 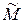 точки
точки 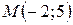 при повороте вокруг начала координат на угол
при повороте вокруг начала координат на угол 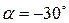 .
.
Решение. Найдем аналитическое выражение поворота, данного в задаче:
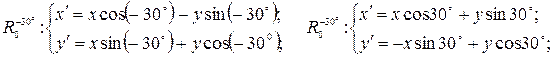
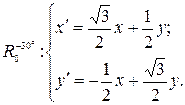
Чтобы найти координаты образа 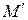 точки
точки 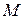 , надо подставить в эти формулы вместо
, надо подставить в эти формулы вместо 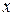 и
и 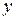 данные координаты точки
данные координаты точки 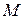 , т.е.
, т.е. 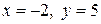 . Тогда
. Тогда 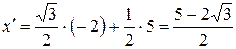 ;
; 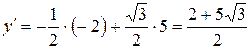 , т.е.
, т.е.
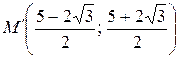 .
.
Чтобы найти координаты прообраза 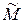 точки
точки 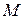 , т.е. координаты точки, для которой
, т.е. координаты точки, для которой 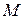 теперь является образом, надо положить
теперь является образом, надо положить 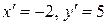 и найти
и найти 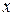 и
и 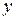 :
:
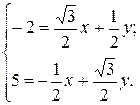
Умножив второе уравнение системы на 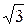 и сложив с первым, найдем
и сложив с первым, найдем 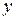 :
:
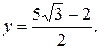
Подставляя найденное значение 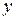 в одно из уравнений системы, найдем
в одно из уравнений системы, найдем 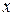 :
:
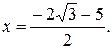
Таким образом, 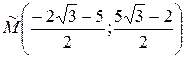 .
.
Ответ: 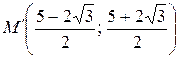 ,
, 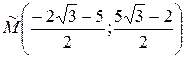 .
.
Задача 1.2. Найти уравнение образа 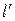 и прообраза
и прообраза 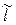 прямой
прямой 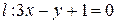 при осевой симметрии с осью
при осевой симметрии с осью 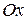 .
.
Решение. Аналитическое выражение осевой симметрии 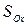 имеет вид:
имеет вид:
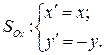
Чтобы найти уравнение образа 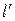 прямой
прямой 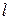 , нужно выразить из этой системы
, нужно выразить из этой системы 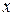 и
и 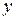 и подставить их в уравнение прямой
и подставить их в уравнение прямой 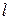 :
:
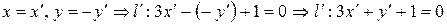 . Опуская штрихи, получаем:
. Опуская штрихи, получаем:
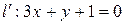 .
.
Чтобы найти уравнение прообраза 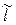 прямой
прямой 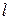 , запишем уравнение прямой
, запишем уравнение прямой 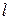 (образа прямой
(образа прямой 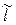 ) в виде
) в виде 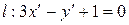 и подставим в него
и подставим в него 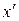 и
и 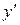 из аналитического выражения
из аналитического выражения 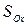 :
:
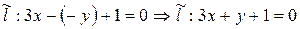 .
.
Получили для прямых 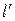 и
и 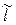 одно и то же уравнение. Это не случайно, т.к. при осевой симметрии (так же как и при центральной) образ и прообраз любой фигуры всегда совпадают.
одно и то же уравнение. Это не случайно, т.к. при осевой симметрии (так же как и при центральной) образ и прообраз любой фигуры всегда совпадают.
Ответ: 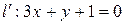 ,
, 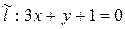 .
.
Задача 1.3. Даны прямые 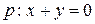 и
и 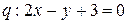 . Найти такие точки
. Найти такие точки 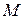 и
и 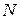 , что
, что 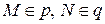 и
и 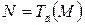 , где
, где 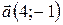 .
.
Решение. 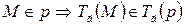 , т.е.
, т.е. 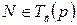 . Тогда учитывая, что
. Тогда учитывая, что 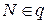 , получаем:
, получаем:
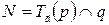 (рис. 18).
(рис. 18).
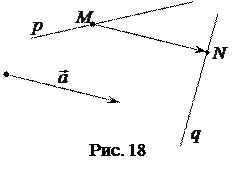 Следовательно, чтобы найти координаты точки
Следовательно, чтобы найти координаты точки 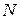 , надо сначала найти уравнение образа
, надо сначала найти уравнение образа 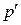 прямой
прямой 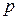 при параллельном переносе на вектор
при параллельном переносе на вектор 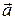 , а затем решить систему уравнений прямых
, а затем решить систему уравнений прямых 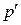 и
и 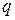 .
.
Найдем аналитическое выражение параллельного переноса на вектор 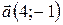 :
:
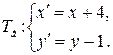
Найдем уравнение образа 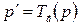 :
:
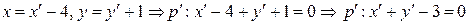 , т.е.
, т.е. 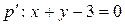 .
.
Решаем систему 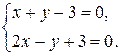
Сложив почленно уравнения системы, получим:
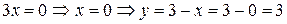 .
.
Итак, 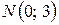 .
.
Так как 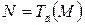 , то
, то 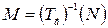 , т.е.
, т.е. 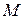 − прообраз точки
− прообраз точки 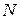 . Найдем координаты прообраза
. Найдем координаты прообраза 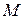 точки
точки 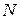 :
:
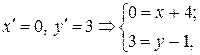
откуда 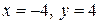 , т.е.
, т.е. 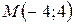 .
.
Ответ: 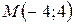 ,
, 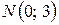 .
.
 2015-06-28
2015-06-28 9466
9466








