Прежде чем приступить к решению задач, дадим несколько методических рекомендаций.
1) При решении задач методом геометрических преобразований часто пользуются следующими утверждениями:
а) 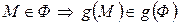 (если точка
(если точка 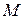 принадлежит фигуре
принадлежит фигуре 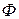 , то ее образ
, то ее образ 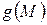 в движении
в движении 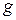 принадлежит образу
принадлежит образу 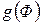 фигуры
фигуры 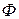 );
);
б) 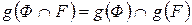 (образ пересечения двух фигур
(образ пересечения двух фигур 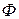 и
и 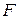 в данном движении
в данном движении 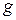 равен пересечению образов этих фигур).
равен пересечению образов этих фигур).
2) Если в задаче дана трапеция, то используется параллельный перенос или гомотетия; если равнобокая трапеция – то осевая симметрия; параллелограмм – центральная симметрия или параллельный перенос; равнобедренный треугольник или угол – осевая симметрия (реже поворот); окружность – осевая симметрия или поворот; равносторонний треугольник или квадрат – поворот вокруг центра или вокруг одной из вершин; равнобедренный прямоугольный треугольник – поворот вокруг вершины прямого угла; две окружности равных радиусов – осевая симметрия или параллельный перенос; две касающиеся окружности равных радиусов – центральная симметрия; параллельные отрезки разной длины или две окружности неравных радиусов – гомотетия.
3) Не спешите с выбором преобразования, сначала проанализируйте условие и требование задачи: выделите фигуры, о которых идет речь в задаче, отношения, которыми они связаны; вспомните свойства и признаки понятий, содержащихся в требовании задачи; рассмотрите связь фигур, заданных в условии, с движениями или гомотетией. Только после этого приступайте к использованию конкретного вида преобразования.
Задача 1.1. Доказать, что сумма боковых сторон трапеции больше разности ее оснований.
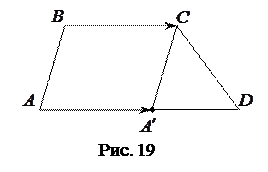 Решение. Пусть
Решение. Пусть 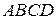 − трапеция,
− трапеция, 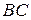 − ее верхнее основание,
− ее верхнее основание, 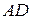 − нижнее (рис. 19).
− нижнее (рис. 19).
Докажем, что 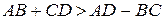 . Подвергнем параллельному переносу
. Подвергнем параллельному переносу 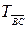 на вектор
на вектор 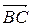 сторону
сторону 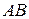 . Тогда
. Тогда 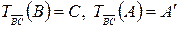 , где
, где 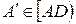 и
и 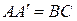 .
.
Получим вспомогательный треугольник 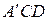 , для которого справедливо неравенство треугольника:
, для которого справедливо неравенство треугольника: 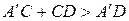 .
.
Так как 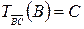 и
и 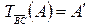 , то
, то 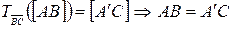 . Поэтому
. Поэтому 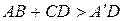 . Так как
. Так как 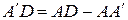 , а
, а 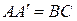 (это равенство вытекает из того, что
(это равенство вытекает из того, что 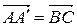 по определению параллельного переноса), то
по определению параллельного переноса), то 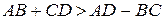 . Неравенство доказано.
. Неравенство доказано.
Задача 1.2. На сторонах 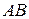 и
и 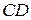 параллелограмма
параллелограмма 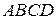 во внешнюю сторону построены равносторонние треугольники
во внешнюю сторону построены равносторонние треугольники 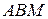 и
и 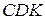 . Доказать, что точки
. Доказать, что точки 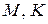 и
и 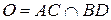 лежат на одной прямой.
лежат на одной прямой.
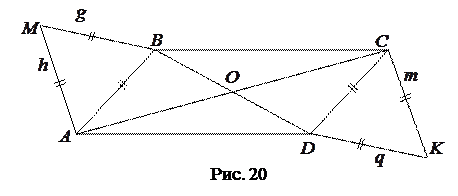 Решение. Для доказательства того, что три точки лежат на одной прямой, используют центральную симметрию или гомотетию. Так как в задаче дан параллелограмм, то воспользуемся центральной симметрией относительно точки
Решение. Для доказательства того, что три точки лежат на одной прямой, используют центральную симметрию или гомотетию. Так как в задаче дан параллелограмм, то воспользуемся центральной симметрией относительно точки 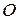 пересечения его диагоналей (рис. 20). Докажем, что
пересечения его диагоналей (рис. 20). Докажем, что 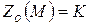 .
.
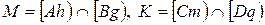 . Найдем образы лучей
. Найдем образы лучей 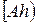 и
и 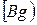 .
.
Так как 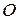 − середина
− середина 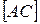 , то
, то 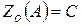 . Так как
. Так как 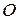 − середина
− середина 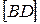 , то
, то 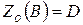 . Тогда
. Тогда 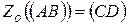 .
.
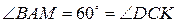 и сторона
и сторона 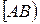 угла
угла 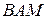 при центральной симметрии
при центральной симметрии 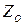 переходит в сторону
переходит в сторону 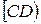 угла
угла 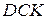 , тогда вторая сторона
, тогда вторая сторона 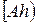 угла
угла 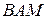 перейдет в сторону
перейдет в сторону 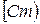 угла
угла 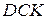 , т.е.
, т.е. 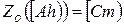 .
.
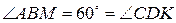 и сторона
и сторона 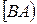 угла
угла 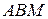 при
при 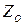 переходит в сторону
переходит в сторону 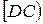 угла
угла 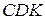 , тогда вторая сторона
, тогда вторая сторона 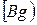 угла
угла 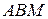 перейдет в сторону
перейдет в сторону 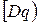 угла
угла 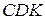 , т.е.
, т.е. 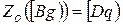 .
.
Тогда применяя равенство б), получим:
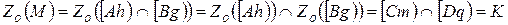 , т.е.
, т.е. 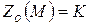 . Следовательно, по определению центральной симметрии точки
. Следовательно, по определению центральной симметрии точки 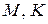 и
и 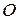 лежат на одной прямой.
лежат на одной прямой.
Задача 1.3. На сторонах 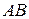 и
и 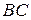 равностороннего треугольника
равностороннего треугольника 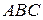 взяты соответственно точки
взяты соответственно точки 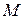 и
и 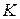 так, что
так, что 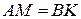 . Найти величину угла между прямыми
. Найти величину угла между прямыми 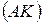 и
и 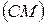 .
.
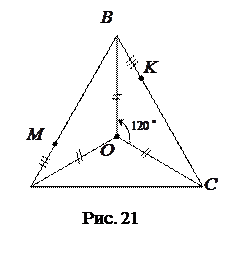 Решение. Центр
Решение. Центр 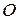 правильного треугольника
правильного треугольника 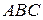 равноудален от всех его вершин (т.е.
равноудален от всех его вершин (т.е. 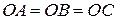 ),
), 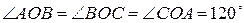 (рис. 21). Рассмотрим поворот вокруг точки
(рис. 21). Рассмотрим поворот вокруг точки 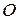 на угол
на угол 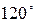 .
.
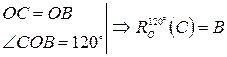 .
.
|
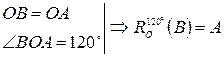 .
. Тогда 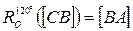 .
.
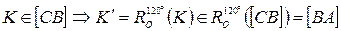 .
.
Так как поворот сохраняет расстояние, то 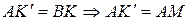 .
.
Итак,
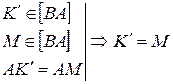 , т.е.
, т.е. 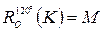 .
.
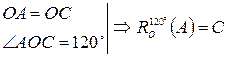 .
.
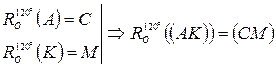 .
.
Учитывая, что угол поворота тупой, делаем вывод, что угол между прямой 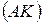 и ее образом
и ее образом 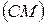 равен
равен 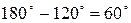 .
.
Ответ: угол между прямыми 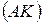 и
и 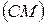 равен
равен 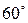 .
.
 2015-06-28
2015-06-28 1036
1036