Раздел «Преобразования плоскости»
Тема 6. Движения. Свойства движений
Типовые задачи с решениями
Задача 1.1. Построить образ окружности 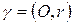 при скользящей симметрии, заданной вектором
при скользящей симметрии, заданной вектором 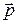 и осью
и осью 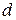 , где
, где 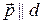 (рис. 6).
(рис. 6).
 Решение.
Решение.
По определению скользящей симметрии сначала строим образ окружности 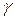 при параллельном переносе
при параллельном переносе 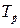 , т.е.
, т.е. 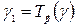 (для этого достаточно построить образ
(для этого достаточно построить образ 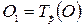 центра
центра 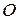 окружности
окружности 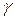 , а радиус окружности
, а радиус окружности 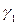 равен
равен 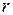 ). Заметим, что окружность
). Заметим, что окружность 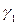 строить не обязательно, достаточно построить ее центр
строить не обязательно, достаточно построить ее центр 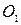 .
.
Затем строим образ 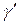 окружности
окружности 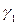 при осевой симметрии
при осевой симметрии 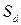 , т.е.
, т.е. 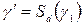 .
.
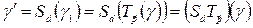 , следовательно,
, следовательно, 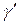 − искомая окружность.
− искомая окружность.
Задача 1.2. На окружности 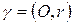 отмечены три точки
отмечены три точки 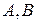 и
и 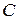 так, что точка
так, что точка 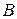 делит пополам дугу
делит пополам дугу 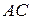 . Доказать, что
. Доказать, что 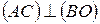 .
.
 Решение. Так как
Решение. Так как 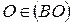 , то
, то 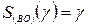 , причем дуга
, причем дуга 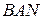 отобразится на дугу
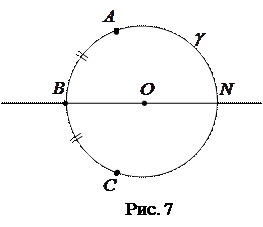
отобразится на дугу 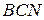 (рис. 7). Тогда точка
(рис. 7). Тогда точка 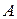 перейдет в такую точку
перейдет в такую точку 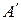 на дуге
на дуге 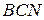 , что дуги
, что дуги 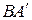 и
и 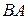 будут равны. А так как по условию
будут равны. А так как по условию 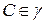 и
и 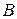 − середина
− середина 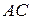 , то точка
, то точка 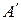 совпадет с
совпадет с 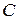 , т.е.
, т.е. 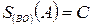 .
.
Тогда по определению осевой симметрии 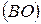 есть серединный перпендикуляр к отрезку
есть серединный перпендикуляр к отрезку 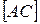 , т.е.
, т.е. 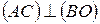 .
.
Задача 1.3. Доказать, что при центральной симметрии прямая, проходящая через центр симметрии, переходит в себя, а прямая, не проходящая через центр симметрии, переходит в параллельную ей прямую.
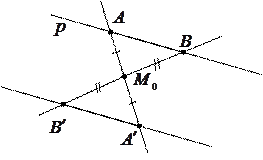 Решение. а) Пусть
Решение. а) Пусть 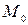 − центр симметрии и прямая
− центр симметрии и прямая 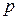 проходит через точку
проходит через точку  (рис. 8, а).
(рис. 8, а).
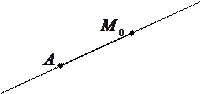 | |||||||||
| |||||||||
| |||||||||
| |||||||||
| |||||||||
Возьмем на прямой 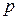 произвольную точку
произвольную точку 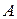 . Пусть
. Пусть 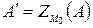 . Тогда по определению центральной симметрии
. Тогда по определению центральной симметрии 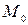 − середина отрезка
− середина отрезка 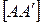 . Следовательно,
. Следовательно, 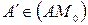 .
.
Так как 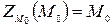 , то
, то 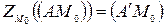 . Учитывая, что
. Учитывая, что 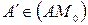 , получаем, что
, получаем, что 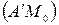 совпадает с
совпадает с 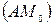 , т.е.
, т.е. 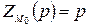 .
.
б) Пусть 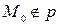 (рис. 8, б). Возьмем точки
(рис. 8, б). Возьмем точки 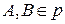 и найдем
и найдем 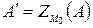 и
и 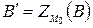 . Тогда
. Тогда 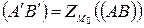 .
.
Диагонали 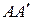 и
и 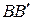 четырехугольника
четырехугольника 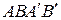 пересекаются и точкой пересечения делятся пополам. Следовательно,
пересекаются и точкой пересечения делятся пополам. Следовательно, 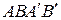 − параллелограмм, откуда получаем, что
− параллелограмм, откуда получаем, что 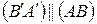 , т.е.
, т.е. 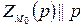 .
.
 2015-06-28
2015-06-28 1102
1102







