2.1. Доказать, что сумма оснований трапеции меньше суммы ее диагоналей.
2.2. Окружность, центром которой является точка биссектрисы 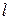 данного угла, пересекает стороны этого угла в точках
данного угла, пересекает стороны этого угла в точках 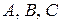 и
и 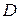 . Доказать, что: а)
. Доказать, что: а) 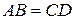 ; б)
; б) 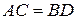 ; в)
; в) 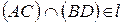 ; г)
; г) 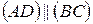 .
.
2.3. Дан квадрат 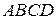 . Через его центр проведены две взаимно перпендикулярные прямые
. Через его центр проведены две взаимно перпендикулярные прямые 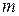 и
и 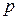 , отличные от прямых
, отличные от прямых 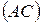 и
и 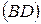 . Доказать, что отрезки, высекаемые квадратом на прямых
. Доказать, что отрезки, высекаемые квадратом на прямых 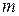 и
и 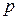 , равны.
, равны.
2.4. На сторонах параллелограмма 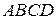 во внешнюю сторону построены квадраты
во внешнюю сторону построены квадраты 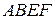 ,
, 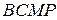 ,
, 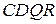 и
и 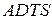 . Доказать, что
. Доказать, что 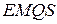 − параллелограмм.
− параллелограмм.
2.5. Даны две равные окружности, касающиеся внешним образом в точке 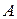 . Через точку
. Через точку 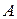 проведена прямая, пресекающая данные окружности в точках
проведена прямая, пресекающая данные окружности в точках 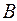 и
и 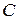 . Через точки
. Через точки 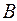 и
и 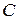 проведены касательные
проведены касательные 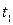 и
и 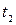 . На них отложены отрезки
. На них отложены отрезки 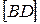 и
и 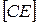 так, что
так, что 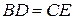 и точки
и точки 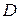 и
и 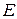 лежат по разные стороны от прямой
лежат по разные стороны от прямой 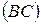 . Доказать, что: а)
. Доказать, что: а) 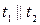 ; б) точки
; б) точки 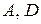 и
и 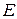 лежат на одной прямой.
лежат на одной прямой.
2.6. Окружности с центрами 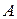 и
и 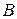 имеют равные радиусы. Доказать, что прямая, параллельная
имеют равные радиусы. Доказать, что прямая, параллельная 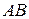 и пересекающая эти окружности, высекает в них равные хорды. Решить задачу двумя способами (т.е. с помощью двух различных движений).
и пересекающая эти окружности, высекает в них равные хорды. Решить задачу двумя способами (т.е. с помощью двух различных движений).
2.7. Дана прямая 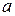 и точки
и точки 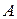 и
и 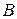 , лежащие по одну сторону от нее. Доказать, что на прямой
, лежащие по одну сторону от нее. Доказать, что на прямой 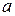 существует единственная точка
существует единственная точка 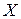 такая, что
такая, что 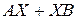 имеет наименьшее значение.
имеет наименьшее значение.
2.8. На сторонах 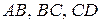 и
и 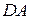 квадрата
квадрата 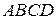 от вершин
от вершин 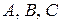 и
и 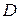 отложены равные отрезки
отложены равные отрезки 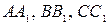 и
и 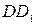 . Доказать, что четырехугольник
. Доказать, что четырехугольник 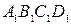 − квадрат.
− квадрат.
 2015-06-28
2015-06-28 756
756








