2.1. Построить образ луча 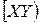 при гомотетии с центром в точке
при гомотетии с центром в точке 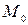 , не лежащей на прямой
, не лежащей на прямой 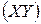 , и коэффициентом
, и коэффициентом 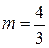 .
.
2.2. Построить образы окружности 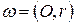 , где
, где 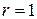 , при гомотетиях
, при гомотетиях 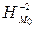 и
и 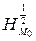 , если
, если 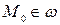 .
.
2.3. Найти уравнения образа 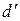 и прообраза
и прообраза 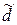 прямой
прямой 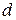 в гомотетии с центром в начале координат и коэффициентом
в гомотетии с центром в начале координат и коэффициентом 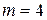 , если: а)
, если: а) 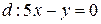 ; б)
; б) 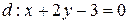 .
.
2.4. Даны две прямые 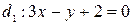 и
и 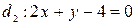 . Найти координаты точек
. Найти координаты точек 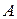 и
и 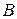 таких, что
таких, что 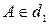 ,
, 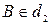 и
и 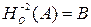 .
.
2.5. Даны точки 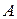 и
и 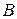 . Найти центр
. Найти центр 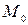 гомотетии
гомотетии 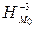 , переводящей
, переводящей 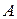 в
в 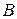 .
.
2.6. Через точку 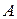 внешнего касания двух окружностей
внешнего касания двух окружностей 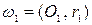 и
и 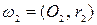 неравных радиусов проведены две прямые
неравных радиусов проведены две прямые 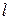 и
и 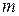 ,
, 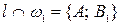 ,
, 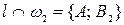 ,
, 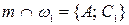 ,
, 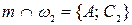 ,
, 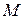 - середина отрезка
- середина отрезка 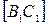 ,
, 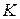 – середина отрезка
– середина отрезка 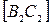 . Доказать, что
. Доказать, что 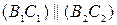 и точки
и точки 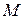 ,
, 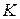 и
и 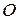
 лежат на одной прямой.
лежат на одной прямой.
2.7. 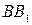 – медиана треугольника
– медиана треугольника 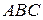 , прямая
, прямая 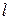 параллельна
параллельна 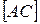 ,
, 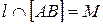 ,
, 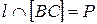 . Доказать, что точка пересечения отрезков
. Доказать, что точка пересечения отрезков 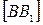 и
и 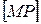 является серединой
является серединой 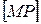 .
.
 2015-06-28
2015-06-28 1116
1116








