2015-06-28
7602
Задача 1.1. Построить образ треугольника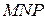 
при гомотетии с центром 
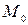и коэффициентом 
.
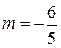Решение. Для построения образа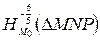 
треугольника 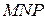следует воспользоваться определением гомотетии. При гомотетии 
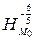точка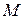 
перейдет в такую точку 
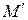, что
;
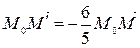точка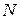 
− в такую точку 
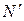, что
;
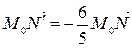а точка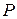 
− в такую точку 
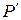, что
.
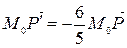Построим образ 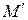точки .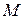
Так как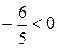 
, то точка лежит между точками и .
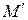Так как
,
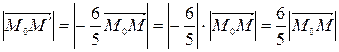то отрезок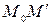 
составляет 
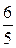отрезка 
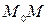. Учитывая все эти выводы, строим точку 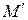(рис. 22).
Проводя аналогичные рассуждения для точек 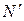и 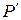, строим эти точки (рис. 22).
 |
.
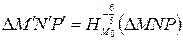Задача 1.2. Найти координаты образа 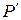и прообраза 
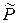точки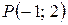 
в гомотетии с центром 
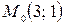и коэффициентом 
.
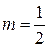Решение. Воспользуемся аналитическим выражением гомотетии:
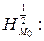
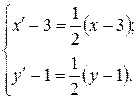
Чтобы найти координаты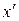 
и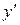 
образа 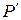точки 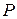, надо положить 
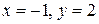. Тогда
.
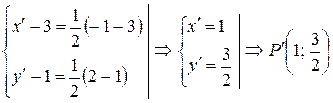Чтобы найти координаты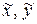 
прообраза 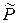точки 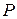(которая для 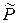является образом), можно записать формулы данной гомотетии в виде:
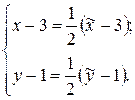
Полагая 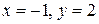, находим 
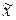и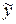 
:
.
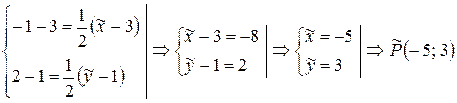Ответ: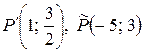 
.
Задача 1.3. Через точку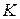 
внешнего касания двух окружносте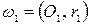й 
и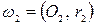 
неравных радиусов проведены две прямые 
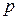и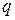 
, 
, 
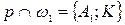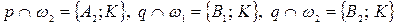. Доказать, что четырехугольник 
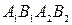есть трапеция.
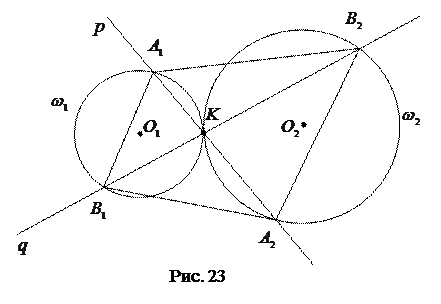Решение. Чтобы доказать, что 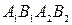− трапеция, достаточно доказать, что 
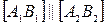и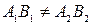 
(так как если бы 
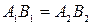, то четырехугольник 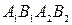был бы параллелограммом) (рис. 23).
Так как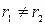 
, то удобно воспользоваться гомотетией. Рассмотрим гомотетию 
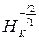с центром в точке 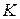и коэффициентом 
.
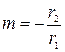Так как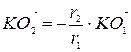 
, то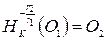 
, а так как отношение радиусов окружностей 
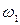и 
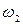равн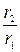о 
, то 
.
Так как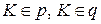 
, то 
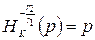и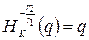 
(по свойству гомотетии).
, 
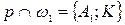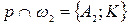. Тогда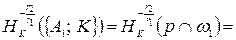 
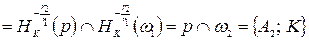. Отсюда и из того, что 
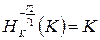, следует, что 
.
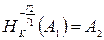Аналогично доказывается, что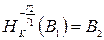 
(предлагаем читателю проделать это самостоятельно).
Таким образом,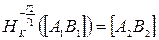 
.
Так как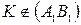 
, то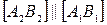 
(по свойству гомотетии).
Так как 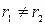,т.е. 
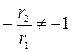, то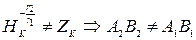 
(данная гомотетия не является движением).
Следовательно, 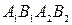− трапеция.
