3.1. Доказать, что разность оснований трапеции больше разности ее боковых сторон.
3.2. Основания трапеции равны 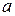 и
и 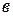 (
(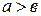 ). Найти длину отрезка, соединяющего середины диагоналей трапеции.
). Найти длину отрезка, соединяющего середины диагоналей трапеции.
3.3. Две прямые 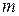 и
и 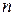 , содержащие точку пересечения диагоналей параллелограмма, пересекают его стороны соответственно в точках
, содержащие точку пересечения диагоналей параллелограмма, пересекают его стороны соответственно в точках 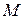 и
и 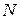 ,
, 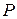 и
и 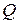 . Доказать, что
. Доказать, что 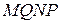 − параллелограмм.
− параллелограмм.
3.4. Через центр правильного шестиугольника проведены две прямые 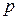 и
и 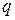 , угол между которыми равен
, угол между которыми равен 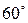 . Доказать, что отрезки этих прямых, заключенные между сторонами шестиугольника, равны.
. Доказать, что отрезки этих прямых, заключенные между сторонами шестиугольника, равны.
3.5. На боковых сторонах 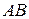 и
и 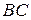 равнобедренного треугольника
равнобедренного треугольника 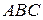 построены равносторонние треугольники
построены равносторонние треугольники 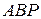 и
и 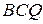 во внешнюю сторону. Доказать, что: а)
во внешнюю сторону. Доказать, что: а) 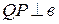 (
(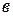 − биссектриса угла
− биссектриса угла 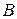 ); б)
); б) 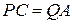 ; в)
; в) 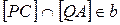 .
.
3.6. На сторонах 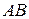 и
и 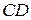 параллелограмма
параллелограмма 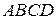 вне его построены правильные треугольники
вне его построены правильные треугольники 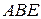 и
и 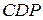 , а на сторонах
, а на сторонах 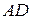 и
и 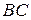 (также вне параллелограмма) – квадраты
(также вне параллелограмма) – квадраты 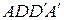 и
и 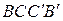 с центрами
с центрами 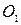 и
и 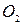 . Доказать, что
. Доказать, что 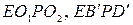 и
и 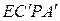 − параллелограммы.
− параллелограммы.
3.7. Прямая 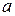 , содержащая точку
, содержащая точку 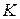 , в которой касаются две равные окружности, пересекает окружности в точках
, в которой касаются две равные окружности, пересекает окружности в точках 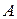 и
и 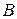 . Доказать, что
. Доказать, что 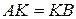 .
.
3.8. Две окружности 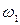 и
и 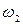 равных радиусов с центрами
равных радиусов с центрами 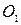 и
и 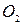 касаются в точке
касаются в точке 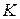 . Через точку
. Через точку 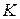 проведены две прямые
проведены две прямые 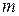 и
и 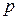 так, что
так, что 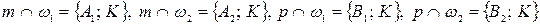 . Доказать, что
. Доказать, что 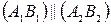 и
и 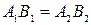 .
.
3.9. Две точки 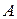 и
и 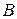 расположены по разные стороны от прямой
расположены по разные стороны от прямой 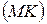 . На прямой
. На прямой 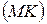 найти точку
найти точку 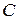 такую, что
такую, что 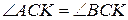 .
.
 2015-06-28
2015-06-28 1084
1084








