Задача 1.1. Аффинное преобразование плоскости задано тремя парами соответственных точек 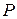 и
и 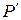 ,
, 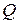 и
и 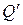 ,
, 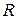 и
и 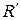 (рис. 24). Построить образ точки
(рис. 24). Построить образ точки 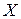 .
.
Решение. Пусть 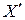 – образ точки
– образ точки 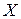 ,
, 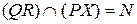 . Проводим прямую
. Проводим прямую 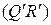 и строим точку
и строим точку 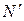 так, чтобы (
так, чтобы (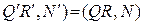 .
.
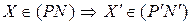 .
.
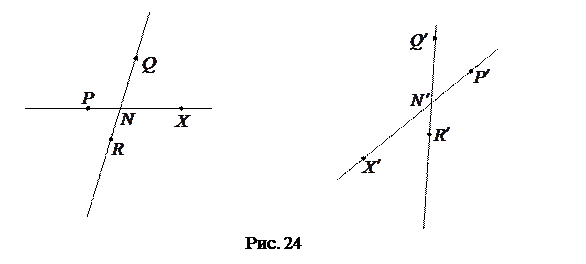
Проводим прямую 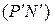 и строим точку
и строим точку 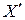 так, чтобы
так, чтобы 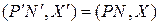 .
.
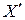 – образ точки
– образ точки 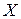 в данном аффинном преобразовании.
в данном аффинном преобразовании.
Задача 1.2. Найти аналитическое выражение аффинного преобразования 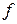 , переводящего репер
, переводящего репер 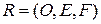 в репер
в репер 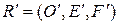 , если
, если 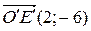 ,
, 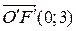 ,
, 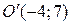 в системе координат
в системе координат 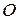 ,
, 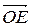 ,
,  . Определить род аффинного преобразования
. Определить род аффинного преобразования 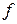 .
.
Решение. Аналитическое выражение аффинного преобразования 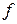 имеет вид:
имеет вид:
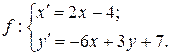
Тогда 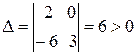 , следовательно,
, следовательно, 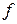 – аффинное преобразование первого рода.
– аффинное преобразование первого рода.
Задача 1.3. Построить образ отрезка 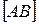 в родстве
в родстве 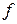 , заданном осью
, заданном осью 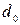 и парой соответственных точек
и парой соответственных точек 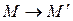 .
.
Решение. Построим образы 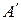 и
и 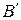 концов отрезка
концов отрезка 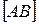 .
.
а) С одной стороны, точка 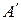 принадлежит прямой
принадлежит прямой 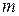 , проходящей через точку
, проходящей через точку 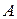 и параллельной
и параллельной 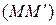 (по свойству
(по свойству 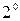 родства) (рис. 25).
родства) (рис. 25).


С другой стороны, если 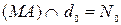 , то точка
, то точка 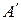 принадлежит прямой
принадлежит прямой 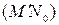 (по свойству
(по свойству 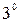 родства).
родства).
Следовательно, 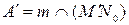 .
.
б) Аналогично строится образ 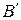 точки
точки 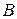 . Опишите это построение самостоятельно (см. рис. 25).
. Опишите это построение самостоятельно (см. рис. 25).
Итак, 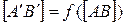 .
.
 2015-06-28
2015-06-28 1052
1052








