2.1. Будут ли два любых параллелограмма аффинно-эквивалентными и почему?
2.2. Аффинное преобразование плоскости задано тремя парами соответственных точек 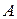 и
и 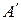 ,
, 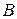 и
и 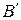 ,
, 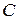 и
и 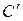 . Построить образ: а) данной точки
. Построить образ: а) данной точки 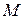 ; б) данной прямой
; б) данной прямой 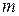 (рис. 26).
(рис. 26).
|


2.3. Можно ли аффинным преобразованием перевести произвольный четырехугольник в четырехугольник, у которого диагонали перпендикулярны и равны? Ответ обосновать.
2.4. Дано аналитическое выражение преобразования плоскости:
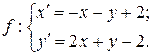
а) Доказать, что 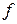 – аффинное преобразование;
– аффинное преобразование;
б) Определить род преобразования 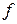 ;
;
в) Найти координаты точки 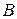 , если
, если 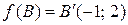 ;
;
г) Найти аналитическое выражение преобразования 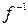 .
.
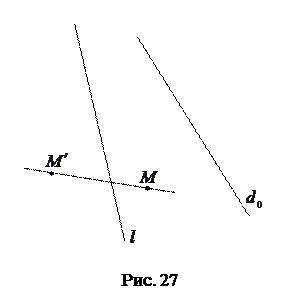 2.5. Построить образ прямой
2.5. Построить образ прямой 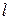 в родстве
в родстве 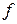 , заданным осью
, заданным осью 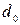 и парой соответственных точек
и парой соответственных точек 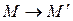 (рис. 27).
(рис. 27).
2.6. Родство 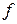 задано осью
задано осью 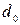 и парой соответственных точек
и парой соответственных точек 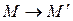 . Построить образ
. Построить образ 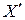 и прообраз
и прообраз 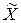 данной точки
данной точки 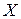 , если
, если 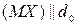 .
.
2.7. Родство 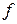 задано осью
задано осью 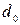 и парой соответственных точек
и парой соответственных точек 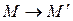 . Построить точки
. Построить точки 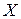 и
и 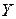 так, чтобы
так, чтобы 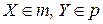 и
и 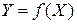 , где
, где 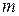 и
и 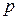 – данные прямые.
– данные прямые. 
 2015-06-28
2015-06-28 602
602








