2015-06-28
1223
3.1. Построить образ угла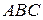 
в гомотетии 
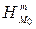(центр гомотетии 
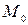не лежит на сторонах угла), если: а) 
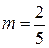; б)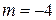 
.
3.2. Даны точк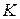и 
и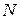 
. Найти центр 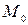гомотетии 
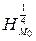, переводящей 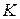в .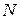
3.3. Найти координаты образа и прообраза точки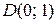 
при гомотетии с центром 
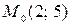и коэффициентом 
.
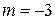3.4.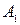 
, 
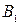и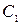 
– середины сторон 
, 
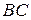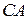и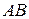 
треугольника 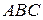соответственно. Доказать, что треугольник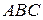и и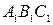 
гомотетичны. Где расположен центр этой гомотетии и чему равен ее коэффициент?
3.5. Две окружности неравных радиусов имеют только одну общую точку. Через нее проведена произвольная секущая. Доказать, что касательные в точках пересечения этой секущей с каждой из окружностей параллельны. Рассмотреть два случая, сделав два чертежа.
