Уравнение вида А х = В, где А, В – выражения, зависящие
от параметров, а х – неизвестное, называется линейным уравнением с параметрами.
Решить уравнение с параметрами – значит для всех значений параметров найти множество всех корней заданного уравнения.
Линейное уравнение А х = В исследуется по следующей схеме.
1) Если А = 0 и В 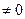 , то уравнение не имеет решений
, то уравнение не имеет решений
(х 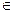 Ø).
Ø).
2) Если А = 0 и В = 0, то уравнение имеет вид 0 · х = 0 и удовлетворяется при любом х, т.е. решением уравнения будет множество всех действительных чисел (х 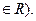
3) Если А 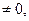 то уравнение имеет единственное решение х =
то уравнение имеет единственное решение х = 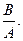
Пример 1. Для всех значений параметров k решить уравнение
(k + 4) х = 2 k + 1.
Решение: Уравнение записано в стандартном виде А х = В, поэтому его исследование проведём по указанной схеме.
1) Если k + 4 = 0, т.е. k = -4, то уравнение имеет вид
0 · х = -7, откуда х 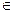 Ø.
Ø.
2) Если k + 4 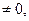 т.е. k
т.е. k 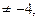 то обе части уравнения можно делить на k + 4. Тогда х =
то обе части уравнения можно делить на k + 4. Тогда х = 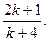
Ответ: если k = -4, то х 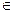 Ø;
Ø;
22
если k 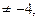 то х =
то х = 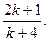
Пример 2. Для всех значений параметров а и b решить уравнение (a – 2) х = 4 а +3 b.
Решение: 1) а = 2. Уравнение имеет вид 0 · х = 8 + 3 b.
Если 8 + 3 b 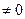 ,т.е. b
,т.е. b 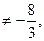 то это равенство ни при каком х не выполняется, поэтому х
то это равенство ни при каком х не выполняется, поэтому х 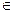 Ø.
Ø.
Если b = - 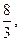 то уравнение примет вид 0 · х = 0, откуда следует: х
то уравнение примет вид 0 · х = 0, откуда следует: х 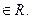
2) а - 2 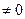 , т.е. а
, т.е. а 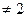 . Тогда х =
. Тогда х = 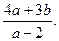
Ответ: если а =2, b 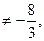 то х
то х 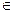 Ø;
Ø;
если а = 2, b = - 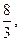 то х
то х 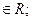
если а 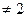 , b - любое, то х =
, b - любое, то х = 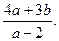
 2015-06-28
2015-06-28 1693
1693
