Определение. Если два числа а и b имеют одинаковые остатки при делении на m, то говорят, что а и b сравнимы по модулю m, и пишут: а 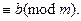
Запись а 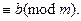 можно прочитать так: а сравнимо с b по модулю m; это означает, что а и b имеют одинаковые остатки при делении на m.
можно прочитать так: а сравнимо с b по модулю m; это означает, что а и b имеют одинаковые остатки при делении на m.
Сравнения – это другая запись свойств делимости. С помощью этой записи можно проще и короче объяснить некоторые из них.
Например, числа 12 и 27 сравнимы по модулю 5
(27 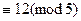 ), так как 27 – 12 =15, а число 15 делится на 5. То же самое можно было объяснить и так: 12 = 5 · 2 + 2, 27 = 5 · 5 + + 2, откуда видно, что 12 и 27 имеют одинаковые остатки при делении на 5.
), так как 27 – 12 =15, а число 15 делится на 5. То же самое можно было объяснить и так: 12 = 5 · 2 + 2, 27 = 5 · 5 + + 2, откуда видно, что 12 и 27 имеют одинаковые остатки при делении на 5.
Свойства сравнений:
1) Сравнимость чисел а и b по модулю m равносильна возможности представить число а виде а = b + mt, где t - целое.
Например, 43 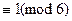 и 43 = 1 + 6 · 7.
и 43 = 1 + 6 · 7.
2) Каждое число а сравнимо с самим собой по произвольному модулю, т.е. а 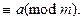
3) Если а ≡ 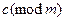 и b ≡ с (mod m), то а
и b ≡ с (mod m), то а 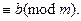
Например, 9 ≡ 5(mod 4) и 13 ≡ 5(mod 4), а, значит,
9 ≡ 13(mod 4).
4) Сравнения с общим модулем можно почленно складывать (или вычитать). Например, 23 ≡ 3(mod 5) и 9 ≡ 24(mod 5),
а следовательно 32 ≡ 27(mod5).
5) Сравнения можно почленно перемножить и возводить в степень, например: 9 ≡ 5(mod 4), следовательно:
а) 90 ≡ 50(mod 4) - обе стороны умножены на 10;
б) 81 ≡ 25(mod 4) – обе стороны возведены в квадрат.
6) Сравнение а 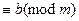 имеет место в том и только в том случае, если разность а – b делится на m.
имеет место в том и только в том случае, если разность а – b делится на m.
Пример 1. Докажите, что число 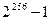 при делении на 7 даёт в
при делении на 7 даёт в
остатке 1.
Решение: Имеем: 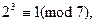
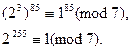
Теперь, умножая обе части полученного сравнения на 2,
получим: 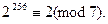
Вычитаем затем 1 из обеих частей последнего сравнения:
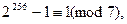
откуда и следует, что число 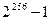 при делении на 7 даёт в
при делении на 7 даёт в
остатке 1.
Пример 2. Найти остаток от деления числа 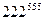 на 7.
на 7.
Решение: Так как 222 = 7 ∙ 31 + 5, то 222 ≡ 5 (mod 7), и поэтому 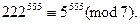
Теперь посмотрим, как повторяются остатки степеней пятёрки при делении на 7. Находим: 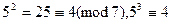 ∙ 5
∙ 5 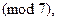
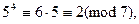
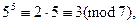
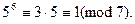 Итак,
Итак, 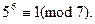 Возводя в степень k, получаем:
Возводя в степень k, получаем: 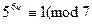 ) при любом натуральном k. Но 555 = 6 · 92+ 3.
) при любом натуральном k. Но 555 = 6 · 92+ 3.
Поэтому 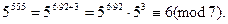
Таким образом, число 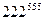 даёт при делении на 7 остаток 6.
даёт при делении на 7 остаток 6.
 2015-06-28
2015-06-28 565
565








