Переход от канонических (параметрических) уравнений прямой к общим не вызывает затруднений. Действительно, если канонические уравнения прямой имеют вид
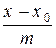
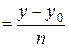
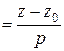 ,
,
то ее параметрические уравнения:
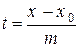 ,
, 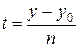 ,
, 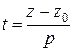
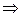
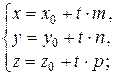
а общие уравнения:
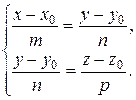
Переход от общих уравнений прямой к каноническим (параметрическим) требует несколько больших усилий.
Пусть прямая 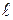 задана общими уравнениями:
задана общими уравнениями:
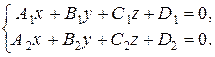 (5)
(5)
Чтобы записать канонические (параметрические) уравнения этой прямой, необходимо найти ее направляющий вектор 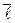 и координаты какой-нибудь точки
и координаты какой-нибудь точки 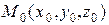 на прямой. Координаты точки
на прямой. Координаты точки 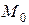 найти легко – это одно из решений системы уравнений (5). Выясним, как можно найти направляющий вектор
найти легко – это одно из решений системы уравнений (5). Выясним, как можно найти направляющий вектор 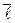 .
.
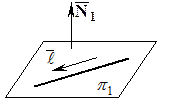 Пусть
Пусть 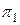 и
и 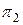 – плоскости, уравнения которых входят в общие уравнения прямой,
– плоскости, уравнения которых входят в общие уравнения прямой, 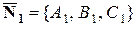 и
и 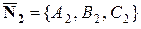 – нормальные векторы к плоскостям
– нормальные векторы к плоскостям 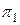 и
и 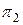 соответственно.
соответственно.
Так как прямая 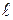 лежит в плоскости
лежит в плоскости 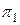 , то векторы
, то векторы 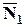 и
и 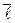 перпендикулярны.
перпендикулярны.
Так как прямая 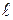 лежит в плоскости
лежит в плоскости 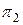 , то векторы
, то векторы 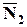 и
и 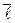 тоже перпендикулярны.
тоже перпендикулярны.
Следовательно, в качестве 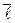 можем взять векторное произведение векторов
можем взять векторное произведение векторов 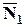 и
и 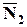 (см. определение векторного произведения в §9).
(см. определение векторного произведения в §9).
ПРИМЕР. Записать канонические уравнения прямой
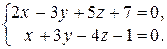 (6)
(6)
1) Найдем одно из решений системы (6). Так как 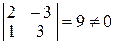 , то этот минор можно выбрать в качестве базисного минора матрицы системы (6). Следовательно, переменные
, то этот минор можно выбрать в качестве базисного минора матрицы системы (6). Следовательно, переменные 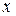 и
и 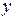 можем выбрать в качестве базисных, а переменную
можем выбрать в качестве базисных, а переменную 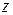 – свободной. Так как нам не нужно все множество решений системы (6), то придадим переменной
– свободной. Так как нам не нужно все множество решений системы (6), то придадим переменной 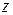 конкретное значение. Например, полагаем
конкретное значение. Например, полагаем 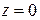 . Тогда переменные
. Тогда переменные 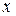 и
и 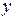 будут удовлетворять системе
будут удовлетворять системе
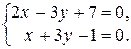
Решаем эту систему по формулам Крамера и получаем:
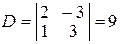 ,
,  ,
, 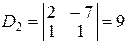 ;
;
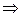
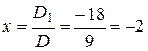 ,
, 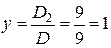 .
.
Таким образом, 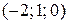 – одно из решений системы (6), и точка
– одно из решений системы (6), и точка 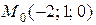 – точка на рассматриваемой прямой.
– точка на рассматриваемой прямой.
2) Найдем направляющий вектор 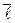 прямой. Имеем:
прямой. Имеем:
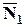
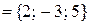 ,
, 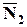
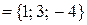 ;
;
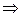
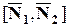
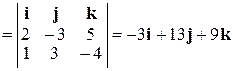 .
.
Следовательно, в качестве направляющего вектора прямой можем взять вектор 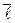
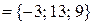 , и канонические уравнения рассматриваемой прямой будут иметь вид:
, и канонические уравнения рассматриваемой прямой будут иметь вид:
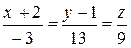 .
.
 2015-06-28
2015-06-28 801
801








