Пусть прямая проходит через точку M 0(x 0; y 0) и имеет направляющий вектор 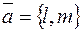 . Тогда для любой ее точки M (x; y) вектор
. Тогда для любой ее точки M (x; y) вектор 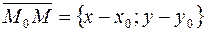 коллинеарен вектору
коллинеарен вектору 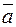 . Это означает, что существует число t такое, что
. Это означает, что существует число t такое, что 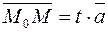 . Записав это равенство в проекциях векторов, получим: x–x 0 =tl, y–y0=tm, или окончательно
. Записав это равенство в проекциях векторов, получим: x–x 0 =tl, y–y0=tm, или окончательно
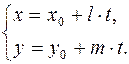 (4)
(4)
Это и есть параметрические уравнения прямой, проходящей через точку M 0(x 0; y 0) в направлении вектора 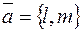 .
.
Замечание 2. Если на параметр t смотреть как на время, то уравнения (4) определяют прямолинейное и равномерное движение точки M (x; y) со скоростью 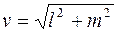 в направлении вектора
в направлении вектора 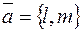 ; точка M 0(x 0; y 0) – начальная (t= 0) точка движения.
; точка M 0(x 0; y 0) – начальная (t= 0) точка движения.
Пример. Составить уравнения движения точки M 0(1;1), движущейся прямолинейно и равномерно в направлении вектора 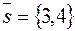 со скоростью
со скоростью 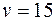 . Установить, в какой момент времени она пересечет прямую
. Установить, в какой момент времени она пересечет прямую
x–y+ 9 = 0.
Решение. Сравнивая модуль вектора 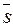 , равный
, равный 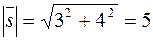 , с заданной скоростью v= 15, мы видим, что в качестве вектора
, с заданной скоростью v= 15, мы видим, что в качестве вектора 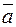 надо взять
надо взять 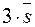 , т.е.
, т.е. 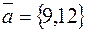 . Тогда искомые уравнения имеют вид:
. Тогда искомые уравнения имеют вид:
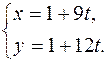 (5)
(5)
В любой момент времени t координаты движущейся точки вычисляются по формулам (5), в частности, и в момент пересечения с прямой x–y+ 9=0. Но в этот момент они должны удовлетворять и уравнению этой прямой, т.е. момент пересечения есть решение уравнения (1+9 t)–(1+12 t)+9=0 или – 3 t+ 9=0. Отсюда t= 3.
IV Полярное уравнение прямой
Если прямая проходит через полюс полярной системы координат и наклонена к полярной оси под углом φ 0, то она определяется совокупностью уравнений 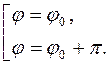
Рассмотрим теперь случай, когда прямая p не проходит через полюс. Пусть M 0(ρ 0; φ 0) – основание перпендикуляра, опущенного из полюса на эту прямую. Возьмем текущую точку M (ρ; φ). В прямоугольном треугольнике
∆M 0 MO угол 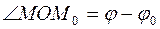
|
|
|
|
|


|

|
 или
или 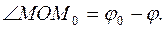 В обоих случаях
В обоих случаях 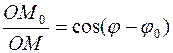 или в более понятной форме
или в более понятной форме 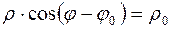 (5)
(5) Это и есть полярное уравнение прямой.
 2015-06-28
2015-06-28 1187
1187
