Опр. Пучок прямых – совокупность всех прямых плоскости, проходящих через некоторую точку S – центр пучка.
Для задания пучка достаточно задать его центр или две любые прямые пучка.
Пусть на плоскости выбрана аффинная система координат и заданы уравнения двух различных прямых
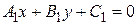 (6.1)
(6.1)
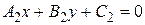 (6.2)
(6.2)
которые пересекаются в точке 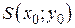 . Рассмотрим уравнение
. Рассмотрим уравнение
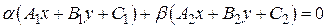 (6.3)
(6.3)
где 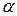 и
и 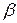 – произвольные действительные числа, не равные одновременно нулю. Покажем, что это уравнение определяет прямую, проходящую через точку S. Перепишем его в виде:
– произвольные действительные числа, не равные одновременно нулю. Покажем, что это уравнение определяет прямую, проходящую через точку S. Перепишем его в виде:
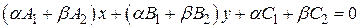 (6.4)
(6.4)
здесь коэффициенты при неизвестных не могут одновременно ровняться нулю. В самом деле, пусть
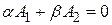 ,
, 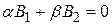 (6.5)
(6.5)
и, например, 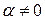 . Тогда и
. Тогда и 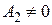 , т.к. из
, т.к. из 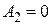 следует
следует 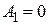 , что противоречит условию пересечения прямых (6.1) и (6.2). Аналогично
, что противоречит условию пересечения прямых (6.1) и (6.2). Аналогично 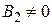 , и равенство (6.5) можно представить в виде:
, и равенство (6.5) можно представить в виде: 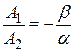 ,
, 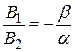 откуда
откуда 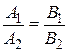 , что невозможно, т.к. прямые (6.1) и (6.2) пересекаются.
, что невозможно, т.к. прямые (6.1) и (6.2) пересекаются.
Прямая (6.3) проходит через точку 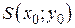 пересечения прямых (6.1) и (6.2), очевидно, т.к. из того, что
пересечения прямых (6.1) и (6.2), очевидно, т.к. из того, что 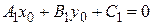 ,
, 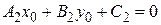 , следует
, следует 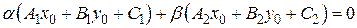 . Пусть
. Пусть 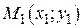 – произвольная точка плоскости, отличная от S. Прямая (6.3) проходит через точку
– произвольная точка плоскости, отличная от S. Прямая (6.3) проходит через точку 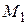 :
:
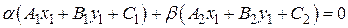 (6.6)
(6.6)
т.к. 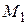 отлична от S, то, по крайней мере, одно из чисел, заключенных в скобки в равенстве (6.6), отлично от нуля.
отлична от S, то, по крайней мере, одно из чисел, заключенных в скобки в равенстве (6.6), отлично от нуля.
Если 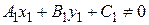 , то равенство (6.6) можно переписать в виде
, то равенство (6.6) можно переписать в виде 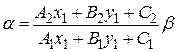 .
.
Уравнение (6.3) – уравнение пучка прямых, определенного прямыми (6.1) и (6.2).
Если заданы координаты центра пучка 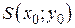 , то уравнение пучка имеет вид
, то уравнение пучка имеет вид 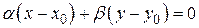 .
.
Пример 6.1. Найти уравнение прямой, принадлежащей пучку прямых 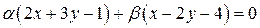 и
и
a) проходящей через точку 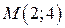 ;
;
b) параллельной прямой 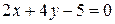 .
.
Решение.
a) Подставив координаты точки 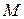 в уравнение пучка прямых найдем значение
в уравнение пучка прямых найдем значение 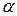 и
и 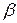 :
: 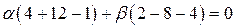 ,
, 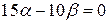 ,
, 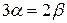 . Пусть
. Пусть 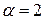 ,
, 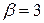 , тогда подставим эти значения в исходное уравнение пучка прямых
, тогда подставим эти значения в исходное уравнение пучка прямых 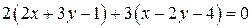 ,
, 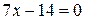 ,
, 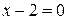 или уравнение прямой принадлежит пучку прямых и проходит через точку
или уравнение прямой принадлежит пучку прямых и проходит через точку 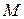 .
.
b) Преобразуем исходное уравнение 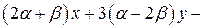
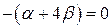 , используя условие параллельности прямых получаем
, используя условие параллельности прямых получаем 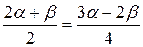 ,
, 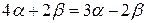 ,
, 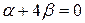 , т.е.
, т.е. 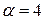 ,
, 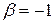 .
.
Подставим эти значения в исходное уравнение пучка прямых 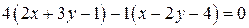 , упрощая получим
, упрощая получим 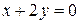 уравнение прямой, принадлежащей пучку прямых и параллельной прямой
уравнение прямой, принадлежащей пучку прямых и параллельной прямой 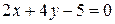 .
.
Ответ.
a) 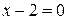 .
.
b) 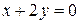 .
.
 2015-06-28
2015-06-28 1174
1174