Прямая на плоскости и различные способы её задания

Пусть ∆- некоторая прямая на плоскости. Любой ненулевой вектор 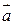, параллельный прямой ∆ называется направляющим вектором этой прямой.

Если задана система координат Оху, направляющий вектор 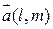прямой ∆ и радиус-вектор 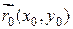некоторой фиксированной точки 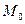прямой ∆, то радиус-вектор 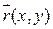произвольной точки M(x,y) этой прямой задаётся формулой:

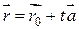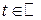, где , (1)

которая называется векторно-параметрическим уравнением прямой ∆.

Из него легко получаются параметрические уравнения прямой в координатах:

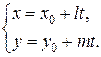(2)

Если 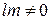то можно записать каноническое уравнение прямой:

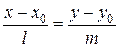(3)

Число 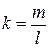(если ∆ не параллельна Oy) называется угловым коэффициентом прямой ∆. Если ∆ 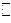Oy, то углового коэффициента не существует. Если 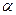-это угол, который образует прямая с положительным направлением оси Ox, то .

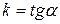Если задан угловой коэффициент k прямой ∆ и некоторая точка M_o(x_o,y_o), то уравнение прямой с угловым коэффициентом можно задать так:

y-y_o=k(x-x_o) (4)

Если M_o(O,b) – это точка пересечения прямой с осью Oy, то это уравнение примет вид: y=kx+b.

Уравнение прямой в отрезках на осях имеет вид:

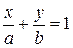, (5)

где а и b соответственно абсцисса и ордината точек пересечения прямой с осями Оx и Оy.

Уравнение прямой, проходящей через две точк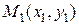и и 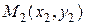имеет вид:

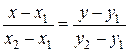(6)

При этом угловой коэффициент прямой, проходящей через точк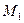и и 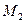, вычисляется по формуле:

.

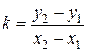Любая прямая может быть задана уравнением:

Ax+By+C=0, (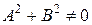), (7)

которое называется общим уравнением прямой. При этом вектор 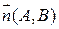ортогонален прямой и называется её нормальным вектором.

----------------------------------------------------------------------------------------------------------------

Прямая на плоскости. Стр. 1