Рассмотрим переход от общего уравнения прямой (10) к каноническим уравнениям (11).
Данный переход осуществляется по АЛГОРИТМУ 1
|
Задача 16 Привести к каноническому виду общее уравнение прямой
|
|
|
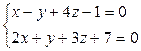 .
.
Решение
Найдём направляющий вектор прямой. Так как он должен быть перпендикулярен нормальным векторам 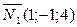 и
и 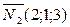 заданных плоскостей, то за
заданных плоскостей, то за 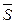 можно принять векторное произведение векторов
можно принять векторное произведение векторов 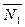 и
и 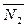 :
:
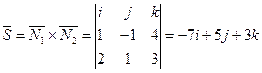
Таким образом, 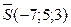
В качестве точки 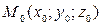 , через которую проходит прямая, можно взять точку пересечения её с любой из координатных плоскостей, например, с плоскостью XOY,так как при этом
, через которую проходит прямая, можно взять точку пересечения её с любой из координатных плоскостей, например, с плоскостью XOY,так как при этом 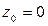 , то
, то 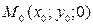 -
- 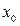 и
и 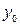 этой точки определяется из системы уравнений заданных плоскостей, если в них положить
этой точки определяется из системы уравнений заданных плоскостей, если в них положить 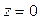 :
:
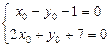
Решая эту систему, находим: 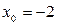 ,
, 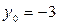 , т.е.
, т.е. 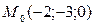
Подставим найденные координаты точки М0 и направляющего вектора S в уравнение (2), получим
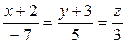 .
.
Ответ: 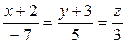
Выполните самостоятельно
Задача 16.1 Привести к каноническому виду общее уравнение прямой:
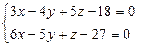
Ответ: 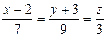 .
.
 2015-06-28
2015-06-28 89331
89331

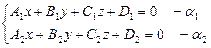 Привести к каноническому виду общее уравнение прямой Решение Выполним схематичный чертеж общего уравнения прямой (рис. 18)
Привести к каноническому виду общее уравнение прямой Решение Выполним схематичный чертеж общего уравнения прямой (рис. 18) 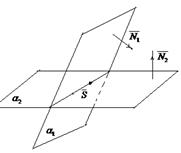 Рис.18 1 Найдем координаты направляющего вектора
Рис.18 1 Найдем координаты направляющего вектора 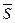 . Так как прямая l лежит в плоскости α1, то вектор
. Так как прямая l лежит в плоскости α1, то вектор 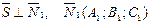 – нормальный вектор плоскости α1. Аналогично
– нормальный вектор плоскости α1. Аналогично 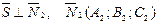 Имеем
Имеем 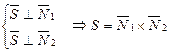 , тогда
, тогда 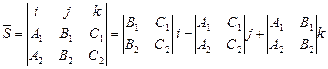 2 Найдем точку М0, через которою проходит прямая. За точку М0 принимают точку пересечения прямой с одной из координатных плоскостей. Пусть М0 = l∩ХОУ, тогда
2 Найдем точку М0, через которою проходит прямая. За точку М0 принимают точку пересечения прямой с одной из координатных плоскостей. Пусть М0 = l∩ХОУ, тогда 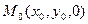 , подставим координаты точки
, подставим координаты точки 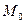 в уравнение (9), получим систему уравнений:
в уравнение (9), получим систему уравнений: 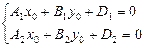 Решим полученную систему, найдем координаты точки
Решим полученную систему, найдем координаты точки 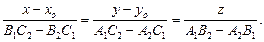 Говорят, чтобы найти точку, через которую проходит прямая нужно одну из переменных в общем уравнение прямой приравнять нулю и решить полученную систему уравнений.
Говорят, чтобы найти точку, через которую проходит прямая нужно одну из переменных в общем уравнение прямой приравнять нулю и решить полученную систему уравнений.