Вычисление координат точки пересечение прямой с плоскостью осуществляется по
АЛГОРИТМУ 2
АЛГОРИТМ 2 Пересечение прямой с плоскостью Дано: l: 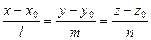 ; α: ; α: 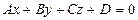 ____________________________ Найти координаты точки пересечения прямой l с плоскостью α (рис.19). Решение ____________________________ Найти координаты точки пересечения прямой l с плоскостью α (рис.19). Решение 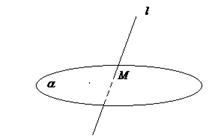 Рис. 19 Пусть прямая l пересекается с плоскостью α в точке М 1 Запишем уравнение прямой l в параметрическом виде Рис. 19 Пусть прямая l пересекается с плоскостью α в точке М 1 Запишем уравнение прямой l в параметрическом виде 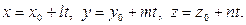 2 Подставим значения х,у,z уравнение плоскости 2 Подставим значения х,у,z уравнение плоскости 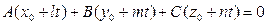 Раскроим скобки и выразим из полученного равенства t Раскроим скобки и выразим из полученного равенства t 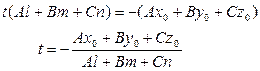 3 Подставим значения t в параметрические уравнения прямой (п.1). Найдем координаты точки М. 3 Подставим значения t в параметрические уравнения прямой (п.1). Найдем координаты точки М. |
Задача17 Найти координаты точки пересечения прямой 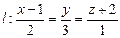 с плоскостью
с плоскостью 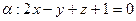 .
.
Решение
Пусть 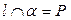
1 Запишем уравнение прямой 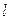 в параметрическом виде:
в параметрическом виде:
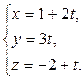
2 Значения x, y, z выраженные через t подставим в уравнение плоскости:
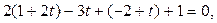
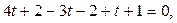
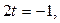
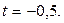
Значение 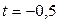 подставим в параметрические уравнения прямой, получим координаты точки
подставим в параметрические уравнения прямой, получим координаты точки 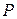 :
:
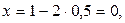
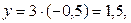
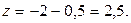
Ответ: 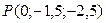
Выполните самостоятельно
Задача17.1 Найти точку пересечения прямой 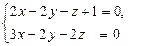
с плоскостью 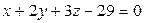 .
.
Замечание. Для решения задачи общее уравнение прямой надо привести к каноническому виду, используя алгоритм 1.
Ответ: (6;4;5)
 2015-06-28
2015-06-28 10516
10516
