АЛГОРИТМ 3 Проекция точки на плоскость Дано: α: 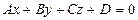 , , 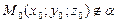 _______________________ Найти проекцию точки _______________________ Найти проекцию точки 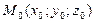 на плоскость α. Решение Выполним схематичный чертеж (рис. 20) на плоскость α. Решение Выполним схематичный чертеж (рис. 20) 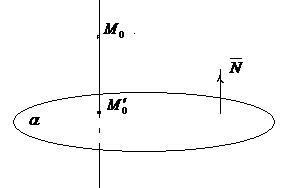 Рис.20 Спроектируем точку Рис.20 Спроектируем точку 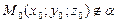 на плоскость на плоскость 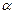 , обозначим проекцию , обозначим проекцию 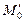 , тогда , тогда 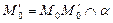 1 Составим уравнение прямой 1 Составим уравнение прямой 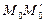 : Т.к. прямая : Т.к. прямая 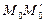 перпендикулярная плоскости перпендикулярная плоскости 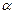 , то за направляющий вектор , то за направляющий вектор 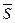 можно взять нормальный вектор плоскости можно взять нормальный вектор плоскости 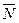 . Тогда . Тогда 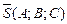 . Подставим координаты точки . Подставим координаты точки 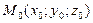 и вектора и вектора 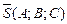 в канонические уравнения прямой, получим в канонические уравнения прямой, получим 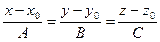 . 2 Найдем координаты . 2 Найдем координаты 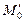 : Т.к. : Т.к. 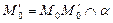 воспользуемся алгоритмом 2 воспользуемся алгоритмом 2 |
Задача19 Найти проекцию точки 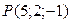 на плоскость
на плоскость 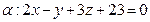
Решение
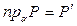 ,
, 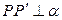
1Составим уравнение прямой 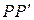 .
.
Прямая 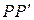 перпендикулярная плоскости, тогда нормальный вектор данной плоскости
перпендикулярная плоскости, тогда нормальный вектор данной плоскости 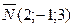 будет являться направляющим вектором искомой прямой.
будет являться направляющим вектором искомой прямой.
Составим уравнение 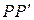 :
:
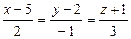
2 Найдем точку пересечения прямой 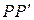 с плоскостью
с плоскостью 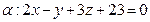 :
:
Воспользуемся алгоритмом 2. Запишем уравнение прямой в параметрическом виде и решим совместно с уравнением плоскости 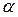
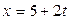 ,
, 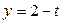 ,
, 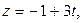
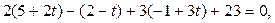
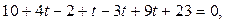
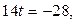
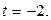
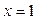 ,
, 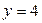 ,
, 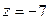
Ответ: 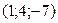
Выполните самостоятельно
Задача 19.1 Составить уравнение перпендикуляра к плоскости 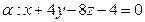 , проходящего через точку А(3;-6;7), и найти координаты основания этого перпендикуляра.
, проходящего через точку А(3;-6;7), и найти координаты основания этого перпендикуляра.
Замечание. Основание перпендикуляра, проведенного из точки А является проекцией точки А на плоскость 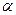 .
.
Ответ: (4; -2; -1)
 2015-06-28
2015-06-28 9656
9656
