АЛГОРИТМ 4 Проекция точки на прямую Дано: 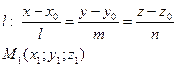 _______________________________________ Найти проекцию точки _______________________________________ Найти проекцию точки 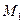 на прямую l Решение Замечание. Проекцией точки на прямую l Решение Замечание. Проекцией точки 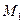 на прямую l является точка на прямую l является точка 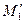 , полученная пересечением прямой l с плоскостьюα, проходящей через точку , полученная пересечением прямой l с плоскостьюα, проходящей через точку 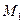 перпендикулярно прямой l (рис. 21) перпендикулярно прямой l (рис. 21) 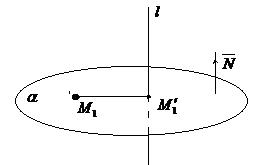 Рис.21 1 Составим уравнение плоскости α. 1.1 Точка Рис.21 1 Составим уравнение плоскости α. 1.1 Точка 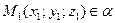 . 1.2 Т.к. прямая . 1.2 Т.к. прямая 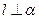 , то за нормальный вектор плоскости α можно взять направляющий вектор прямой l: , то за нормальный вектор плоскости α можно взять направляющий вектор прямой l: 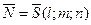 1.3 Составим уравнение плоскости α, получим 1.3 Составим уравнение плоскости α, получим 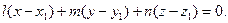 2 Найдем точку пересечения прямой l с плоскостью α по алгоритму 2. 2 Найдем точку пересечения прямой l с плоскостью α по алгоритму 2. |
Задача 20 Найти проекцию точки 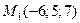 на прямую
на прямую 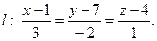
Решение
1 Составим уравнение плоскости α, проходящей через точку 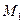 перпендикулярно прямой l (рис. 21)
перпендикулярно прямой l (рис. 21)
1.1 Точка 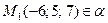 .
.
1.2 Т.к. прямая 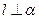 , то за нормальный вектор плоскости α можно взять направляющий вектор прямой l:
, то за нормальный вектор плоскости α можно взять направляющий вектор прямой l: 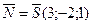
1.3 Составим уравнение плоскости α:
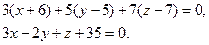
2 Найдем 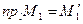 , как точку пересечения прямой l с плоскостью α по алгоритму 2.
, как точку пересечения прямой l с плоскостью α по алгоритму 2.
Запишем уравнение прямой в параметрическом виде:
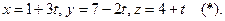
Подставим значения х, у,z в уравнение плоскости и найдем t.
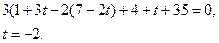
2 Найдем координаты точки 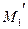 .
.
Подставим значение t в уравнения (*),получим: 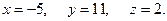
Ответ: 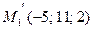
Следствие 1 Расстояние от точки до прямой находится, как длина отрезка между точкой и её проекцией на прямую.
Задача 21 Найти расстояние от точки 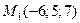 до прямой
до прямой 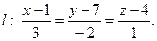
Решение
1Найдем 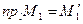 (см. задачу 8),
(см. задачу 8), 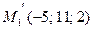 .
.
2 Расстояние от точки 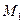 до прямой l найдем, как длину отрезка между точкой и её проекцией на прямую:
до прямой l найдем, как длину отрезка между точкой и её проекцией на прямую: 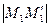 .
.
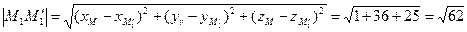
Ответ: 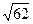
 2015-06-28
2015-06-28 8376
8376
