1) На плоскости. Пусть даны три вектора 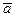 ,
, 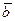 и
и 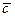 . Разложить вектор
. Разложить вектор 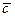 по направлениям
по направлениям 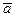 и
и 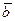 . Через
. Через 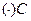 проводим прямые параллельные
проводим прямые параллельные 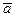 и
и 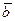 до пересечения с их направлениями. Получаем
до пересечения с их направлениями. Получаем 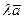 и
и 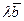 :
: 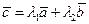 .
.
2) В пространстве: 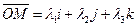 .
.
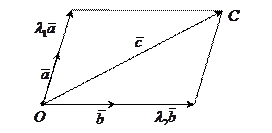 | 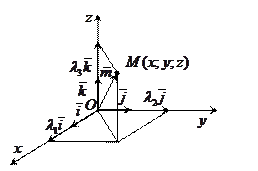 | ||
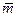 – вектор, который надо разложить по векторам
– вектор, который надо разложить по векторам 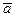 ,
, 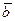 и
и 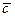 .
.
4.9. Действия над векторами, заданным координатами
в пространстве
1) При сложении векторов, заданных координатами, соответствующие координаты складываются: 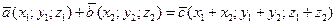 .
.
2) При умножении вектора на число его координаты умножаются на это число: 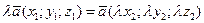 .
.
3) Скалярное произведение векторов равно сумме парных произведений их одноименных координат: 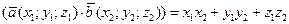 .
.
4) Косинус угла между векторами 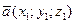 и
и 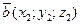 в пространстве находится по формуле:
в пространстве находится по формуле: 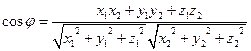 , где
, где
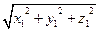 – длина вектора
– длина вектора 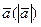 ;
;
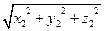 – длина вектора
– длина вектора 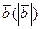 .
.
 2015-06-28
2015-06-28 547
547








