2015-06-28
465
Исследование функций можно провести по следующей схеме:
1. Найти область определения функции.
2. Исследовать изменение функции при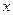 
стремящемся к концам промежутков области определения.
3. Поверить функцию на четность и нечетность (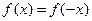
– четная, 
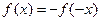– нечетная; 
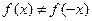и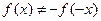 
– общего вида).
4. Проверить, является ли функция периодической.
5. Найти критические точки (вычислить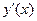 
; решить уравнение 
).
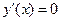6. Найти промежутки возрастания (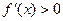
) и убывания 
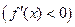функции.
7. Определить точки экстремума, их вид и вычислить значения экстремумов.
8. Определить интервалы выпуклости (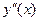
; 
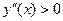– выпуклая вниз; 
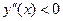– выпуклая вверх) и точки перегиба (
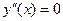или 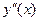не существует).
9. Найти точки пересечения графика функции с осями координат (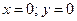
).
10. Вычислить асимптоты кривой если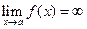 
, то прямая 
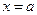– вертикальная асимптота; если 
, 
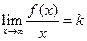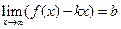, то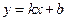 
–наклонная асимптота.
11. Построить график функции.
Правило Лопиталя. Производную можно применять для нахождения пределов отношений вида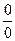 
и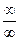 
: предел отношения двух бесконечо малых или бесконечно больших функций равен пределу отношения их производных, если последний существует: 
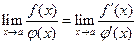. Иногда правило Лопиталя приходится применять несколько раз.
