2015-06-28
733
1. Непосредственное интегрирование:
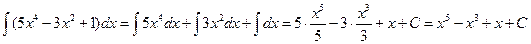
2. Замена переменной интегрирования. Интегрирование путем ведения новой переменной (метод подстановки основан на формул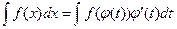е 
, где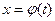 
– функция переменной 
.
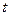3. Интегрирование по частям. Если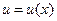 
, 
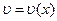– дифференцируемые функции от 
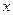, то из формулы дифференциала произведения двух функций 
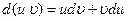получается формула интегрирования по частям:
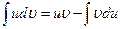
В качестве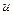 
обычно выбирается функция, которая упрощается дифференцированием, в качестве 
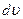– оставшаяся часть подынтегрального выражения, содержащая 
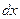, из которой можно определить 
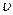путем интегрирования.
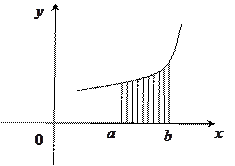Пусть на отрезке 
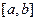определена функция 
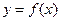. Отрезок 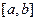разобьем на 
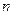частей точками 
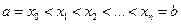. В каждом из отрезков 
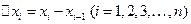произвольным образом выберем точку 
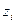и составим сумму произведений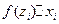 
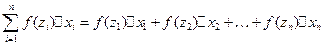
Эта сумма называется интегральной суммой функции 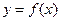в промежутке .
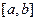Определение: определенным интегралом от функции 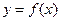в промежутке 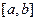называется предел ее интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длинна наибольшего из них стремится к 0.
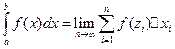
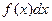– подынтегральное выражение; 
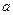и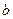 
– пределы интегрирования ( 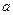– нижний, 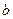– верхний), 
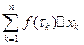– интегральная сумма.
