Формула полной вероятности

Пусть событие А может произойти лишь при условии появления одного из всех n попарно несовместимых событий 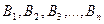, образующих полную группу событий. События 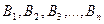будем называть гипотезами для события А. (hypotesis (гр) – основание, предположение). Тогда 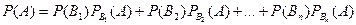– есть формула полной вероятности.

Событии А может наступить только при условии наступления одного из событий 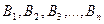, т.е. 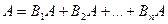. На основании теоремы сложения и умножения вероятностей имеем:

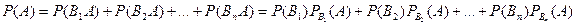
Пример: на экзамен было заготовлено 50 задач: 20 графических и 30 расчетных. Для сдачи зачета студент должен решить первую же доставшуюся наугад задачу. Какова вероятность для студента сдать зачет, если он умеет решать 18 графических и 15 расчетных задач.

Вероятность получить задачу графическую (событие 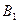) равно 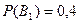, расчетную 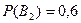. Если событие А означает, что задача решена, то 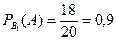, 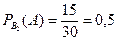. Значит .

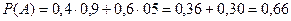14.9. Теорема умножения вероятностей 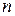независимых событий:

Если события 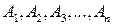независимы, то вероятность их произведения равна произведению вероятностей этих событий:

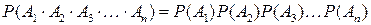
Вычисление вероятности суммы независимых событий: 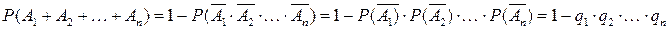где 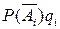. Если независимые события 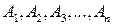имеют одинаковую вероятность, равную 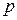, то вероятность появления хотя бы одного из этих событий выражается функцией 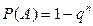, где .