Геометрические вероятности. Классическое определение вероятности предполагает, что число всевозможных исходов – конечно

Классическое определение вероятности предполагает, что число всевозможных исходов – конечно. На практике часто приходится проводить испытания, в которых может происходить бесконечное количество исходов. В таких опытах для вычисления вероятности появления конкретного события классическое определение вероятности неприменимо и вводят геометрические вероятности – вероятности попадания точки в область.

Пусть на плоскости задана с помощью геометрического образа (отрезка, тела, фигуры) конкретная область, имеющая свою меру. Обозначим эту область буквой 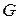. В области 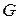содержится область 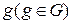. В области 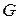наудачу бросается точка. Будем считать, что брошенная точка может попасть в некоторую часть области 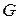с вероятностью, пропорциональной ее величине и независимой от ее формы и расположения. Пусть 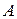– попадание брошенной точки в область 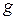, тогда геометрическая вероятность этого события определяется формулой: 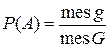, где 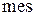– мера области ( 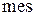– первые три буквы французского слова 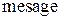, что значит мера). Мера области может быть длинной (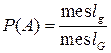), площадью (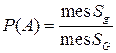), объемом (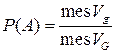), где (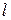) – длина, (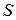) – площадь, (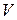) – объем.